Conta a lenda que o xadrez foi inventado na Índia, há mais de 1500 anos. O rei ficou tão fascinado com a invenção e as infinitas variações de movimentos, que resolveu recompensar o inventor.

O rei perguntou: O que você quer de recompensa?
Inventor: Quero um grão de arroz para a primeira casa, dois grãos para a segunda casa, 4 para a terceira, e assim sucessivamente.
“Só isso?”, o rei retrucou.

Então, o rei pediu para os matemáticos do reino fazerem as contas.
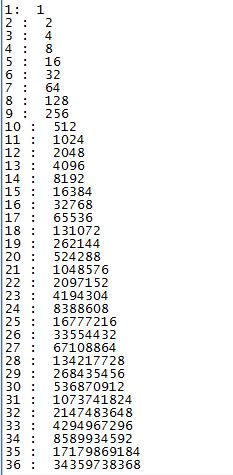
- Na primeira casa, 1 grão = 2^0
- Na segunda casa, 2 grãos = 2^1,
- Na terceira casa, 4 grãos = 2^2.
É uma progressão geométrica. O tabuleiro é um quadriculado de 8×8, portanto tem 64 casas.
A vigésima primeira casa já tem mais de 1 milhão de grãos de arroz!
A casa 41 corresponde a mais de 1 trilhão de grãos de arroz!
E a casa 64, a 9 quinquilhões de grãos!

A soma de todas das casas é igual a 2^64-1 = 1,8 *10^19 grãos de arroz.
Este post recebeu uma série de respostas criativas. Reproduzo algumas a seguir.
Do colega Juliano Santos:
Considerando que 100 grãos de arroz pesam 2,73 gramas (a primeira variedade de arroz apresentada neste site).

https://www.iac.sp.gov.br/areasdepesquisa/graos/arroz.php
O maior avião cargueiro até o presente momento é o “Antonov AN-225 Mriya”, de fabricação Russa e o peso máximo de carga que ele suporta é de 250 tons.
O número de grãos de arroz equivale a 20.143.844.528 aviões “AN-225” (mais de 20 bilhões de AN-225).
Outra conta do Juliano Santos:
A produtividade média do arroz é de 6,2 ton de arroz por hectare. Seriam necessários 812.251.795.503 hectares para produzir esta quantidade de arroz.
Seria necessária uma área equivalente à 2.471 vezes o tamanho da Índia para que o rei pudesse cultivar o arroz necessário para pagar o inventor.
O colega Arthur Bratti calculou uma piscina de 150 km² por 20 m (metros!) de profundidade, para colocar todos esses grãos de arroz. Essa área representa 2.250.000 ha, ou seja, essa piscina gigante ocuparia uma boa parte de Santa Catarina.

O amigo Bruno Cambria fez outras comparações.
Um dos maiores navios cargueiros do mundo carrega 400 mil ton. Seria necessário mais de 1,1 milhão deles para carregar todo esse peso

Se todo arroz produzido no mundo fosse destinado a isso, seriam necessários 633 anos para chegar nesse valor.

Seria necessário o equivalente a 532 Reservas da Cantareira para armazenar todo o arroz.

Se o rio Amazonas fosse esvaziado, preenchido com arroz e mantivesse a mesma vazão, você levaria 45 dias para ver todo o arroz passando na sua frente.
Se 8 pessoas fizessem esse pedido para o rei, o Grand Canyon não seria suficiente para estocar todo o arroz
Este é o poder da Progressão Geométrica.

Notebook no Colab: https://colab.research.google.com/drive/1xoiry4Hzaf5-LPxFVQvOSso2Yoogjtm6?usp=sharing
Outra curiosidade: os amigos da Negociarte, empresa de treinamento, utilizaram exatamente este post para ilustrar o contraste entre pensamento exponencial e linear.
Um último detalhe técnico. O Excel perde um pouco de precisão nas últimas casas decimais, pelo sistema de ponto flutuante. O Python utiliza uma espécie de Big Int, então é mais preciso para fazer essa conta, a rigor.
Veja também:
https://ideiasesquecidas.com/laboratorio-de-matematica/
https://ideiasesquecidas.com/2020/03/09/corona-virus-e-cisnes-negros/
Desafio de xadrez do Instituto Penrose
Negativo vezes negativo igual a positivo. Por quê?
Loja e Recomendações:
Quantos envelopes preciso comprar para completar o álbum da copa?
Código Python:
s=1
print(“1: “, s)
for x in range(1,64):
s = s * 2
print(x+1, “: “, s)


Pingback: O Mito das Regras de Senhas Seguras | COMPUTAÇÕES ANÔMALAS
muito bom!
CurtirCurtir
Posso estar enganado, mas esse conto é do livro “O Homem que Calculava” do matemático brasileiro Malba Tahan.
CurtirCurtido por 1 pessoa
Eu vi a mesma história de várias fontes, uma delas o livro de xadrez do Idel Becker. Nunca li o livro do Malba Tahan.
CurtirCurtir
Uma dúvida:
A casa 64 equivale a sextilhoes ou quinquilhoes?
CurtirCurtir
Acho que é quinquilhão, vou corrigir.
Zero = 0
Milhão = 10^6
Bilhão = 10^9
Trilhão = 10^12
Quadrilhão = 10^15
Quintilhão = 10^18
Sextilhão = 10^21
Septilhão = 10^24
CurtirCurtir
Republicou isso em Forgotten Math.
CurtirCurtir
À partir da casa 50 o seu resultado está errado:
281474976710656 49
562949953421312 50
1125899906842624 51
2251799813685248 52
4503599627370496 53
9007199254740992 54
18014398509481984 55
36028797018963968 56
72057594037927936 57
144115188075855872 58
288230376151711744 59
576460752303423488 60
1152921504606846976 61
2305843009213693952 62
4611686018427387904 63
9223372036854775808 64
Como diz a lenda o valor dobra na casa seguinte, o que é diferente de se elevar 2 ^64.
Um pequeno código em Python resolve o problema:
x = 1
s = 1
print(x)
while x < 64:
s = s * 2
print(s)
x += 1
CurtirCurtido por 1 pessoa
Perfeito, Roberto. O Excel esbarra na precisão finita do tipo inteiro. O python não tem limite, ou melhor, o limite é a capacidade da máquina. Vou corrigir no post. Obrigado.
CurtirCurtir
Talvez este antigo ensinamento seja útil para explicar aos diletantes o que significa uma progressão geométrica e não observar o distanciamento social!
CurtirCurtido por 1 pessoa
Acredito que houve um equivoco ao dizer que essa progressão é geométrica.
Pois como o que está variando é o expoente, essa seria uma progressão exponencial:
F(x) = 2^x
Progressão geométrica seria uma multiplicação:
F(x) = n*x
CurtirCurtir
PG: Cada termo é a multiplicação do anterior por uma constante: http://educacao.globo.com/matematica/assunto/algebra/progressao-geometrica-pg.html, dá uma olhada.
CurtirCurtir
Mas que arroz pesado heimmm!!
Se um grão de arroz pesa um grama então um pacote de arroz de 5 kg contem apenas 5000 grãos de arroz ????
CurtirCurtir
Pingback: Permutações – Forgotten Math
Pingback: Por que ser ágil? - DataChemistry
No delicioso livro O Homem Que Calculava, o matemático e escritor brasileiro Malba Tahan conta lindamente esta história, mas com grãos de trigo em vez de arroz.
CurtirCurtido por 1 pessoa
Pingback: Por que ser ágil? – Práticas Ágeis
Pingback: Pensamento linear, mundo exponencial - Negociarte
Pingback: A magia dos juros compostos | Pra que investir
Pingback: Matemática em jogos clássicos - Klug - Academia de estudos