Um desafiozinho de xadrez, criado pelo Penrose Institute.
É um puzzle relativamente simples de resolver, necessitando de um nível um pouco acima de básico de xadrez.
Entretanto, é muito interessante porque nem os melhores supercomputadores do mundo conseguem resolver.
Nota: Roger Penrose é um físico e matemático extremamente respeitado, tendo desenvolvido diversos trabalhos com o conhecido físico Stephen Hawking, um dos primeiros a propor a ideia de Buracos Negros.
O puzzle:
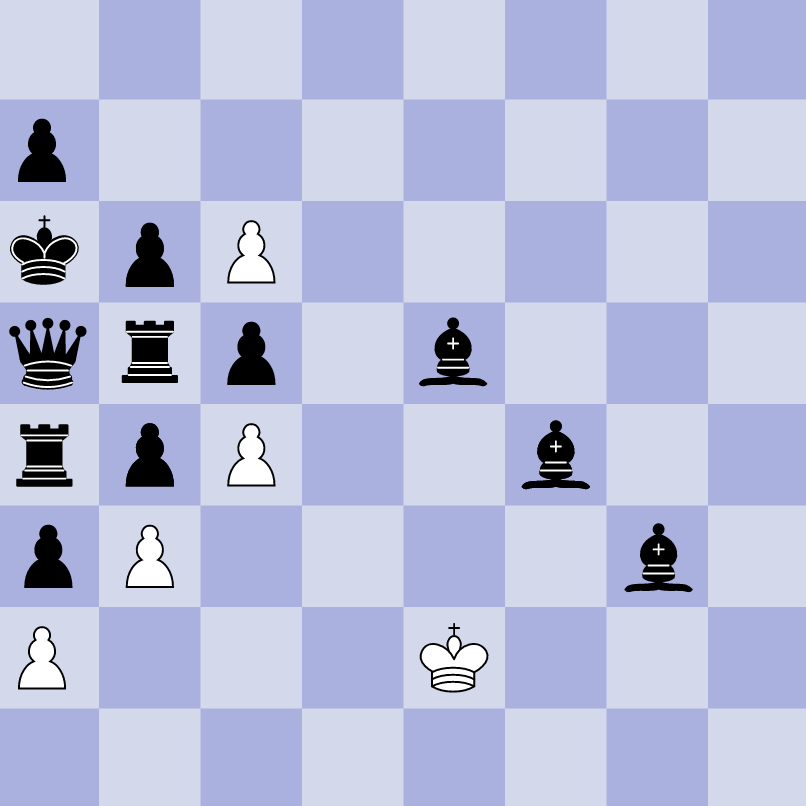
Link original.
Porque é difícil para computadores?
Sabendo como são programados os computadores, sabe-se também como enganá-los.
Xadrez é um jogo em que o número de combinações facilmente explode para infinito. É difícil olhar 2 jogadas à frente, imagine 5, 10, 15 jogadas à frente! Mesmo o computador mais poderoso do mundo não consegue explorar todas as jogadas possíveis de maneira exaustiva, demoraria milhares de anos para tal. Então, como fazer?
Os programas de computador levam em conta aspectos como a força relativa de cada peça (por exemplo, a dama vale mais que o cavalo), a posição (a dama numa posição central tem mais chance de atuar do que presa atrás de um peão), e também um banco de dados gigantesco de boas jogadas e posições.

O xadrez é um jogo conhecido há uns 1500 anos (https://en.wikipedia.org/wiki/History_of_chess). Há séculos, as peças e as regras são as mesmas. Por isso, há centenas de milhares de jogos catalogados, e daí é possível extrair padrões: jogadas de início, meio de jogo, fim de jogo. É como se fossem marcos a serem atingidos numa viagem: para chegar à Índia, primeiro passar pelo Cabo da Boa Esperança, depois pelas ilhas de Madagascar, etc… Isto facilita muito o algoritmo, porque reduz violentamente o número de possibilidades.
Eu não sou nenhum especialista em xadrez, mas só de olhar o tabuleiro, dá para sacar algumas conclusões:
- Em termos de força das peças, as pretas têm muito mais poderio: dama, torre, bispos, enquanto as brancas só tem três peões.
- O posicionamento das peças é muito esquisito. As pretas, que começam o jogo na parte de cima, estão no lado esquerdo do tabuleiro. Esta posição bem unusual é feita de propósito, para evitar que o computador encontre um marco bem definido. É como chegar à Índia começando a viagem do pólo-norte, da onde não se tem rotas definidas.
- As peças brancas, embora fortes, estão todas travadas, e numa posição bem maluca. É extremamente improvável, embora não impossível, ter uma situação dessas.
- Três bispos brancos em casas da mesma cor? Eu já tinha resolvido o puzzle, mas não tinha sacado como seria possível ter três bispos no jogo. Só depois fui perceber: é possível sim, basta avançar um peão branco até a última casa e promover a bispo (também muito unusual).
- Peças brancas fortes, posições esquisitas, tudo é muito estranho, para forçar o computador a abandonar a estratégia de pegar atalhos, fazê-lo percorrer milhões de combinações possíveis e não chegar a lugar nenhum.
Solução:
Minha solução será publicada daqui a uma semana, para dar aos leitores tempo para pensar.
Atualização: já publiquei a solução, aqui.
Para quem resolver, principalmente se tiver alguma ideia muito legal, enviar a solução para puzzles@penroseinstitute.com.
Sugiro parar a leitura para tentar a solução. Mas segue uma dica, se necessário.
Há alguns critérios possíveis para considerar um jogo empatado:
– Stalemate: brancas não tem jogada possível
– Não existe checkmate possível, exemplo quando sobra rei contra rei
– Repetição três vezes seguidas: a mesma jogada é repetida trẽs vezes consecutivas, pelos dois lados
– Regra dos cinquenta movimentos: não há captura ou movimento de peão nos últimos 50 movimentos de cada jogador.
Vide também: https://ideiasesquecidas.com/laboratorio-de-matematica
Nota: Assim como em alguns puzzles anteriores, este me foi passado pelo grande engenheiro Marcos Melo.


Republicou isso em Forgotten Math.
CurtirCurtir
Pingback: Desafio do Penrose Institute – Xadrez na Praça