A progressão geométrica 1 + 2 + 4 + 8 + …, com cada elemento sendo o dobro da anterior, tem soma igual a 2^N-1, onde N é o número de elementos da soma.
Há uma prova visual muito bonita desta.
Imagine que tomamos emprestado um quadrado, o vermelho, e somamos o primeiro elemento (1):
O próximo elemento da soma, o 2, colocamos à direita – espelhando a soma anterior.
O próximo elemento da soma, o 4, é representado abaixo, de novo espelhando a soma anterior.
E assim sucessivamente. Para 8:
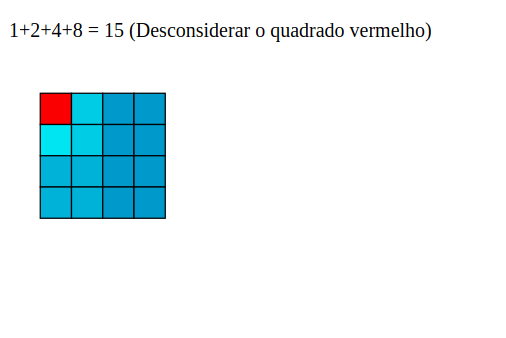
Para o 16:
Com 10 elementos:
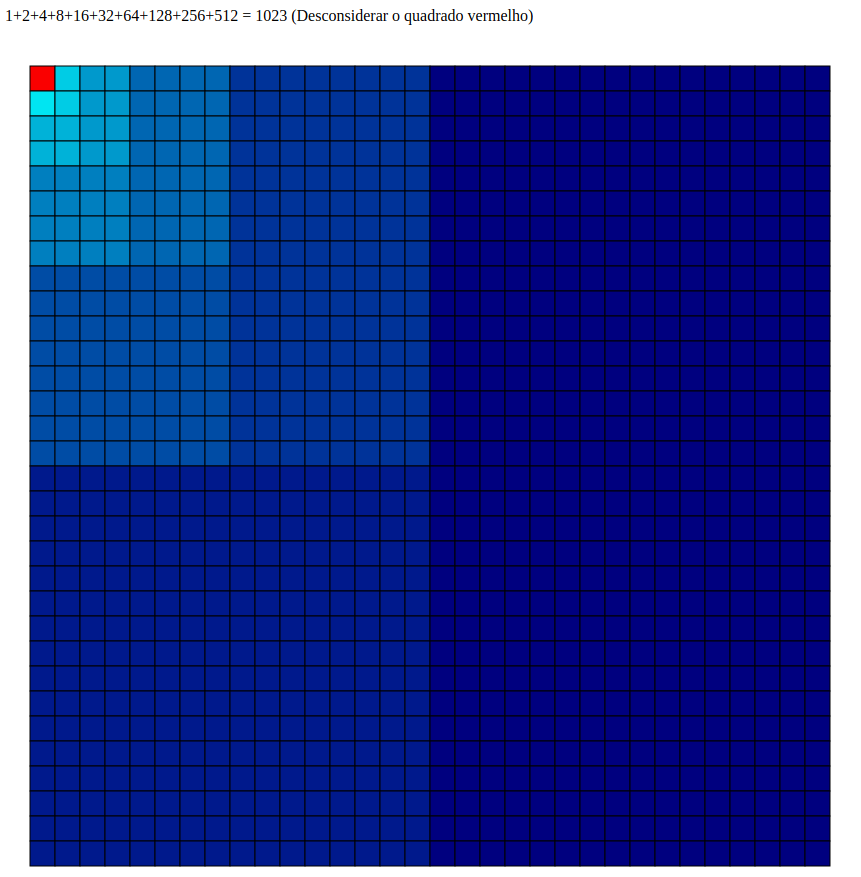
Criei um programinha para visualizar dinamicamente essa soma geométrica. É da onde os prints acima foram tirados. Segue o link:
https://asgunzi.github.io/somageometricaD3
Agora, um pouco da teoria. Uma soma de PG finita é dada pela fórmula:
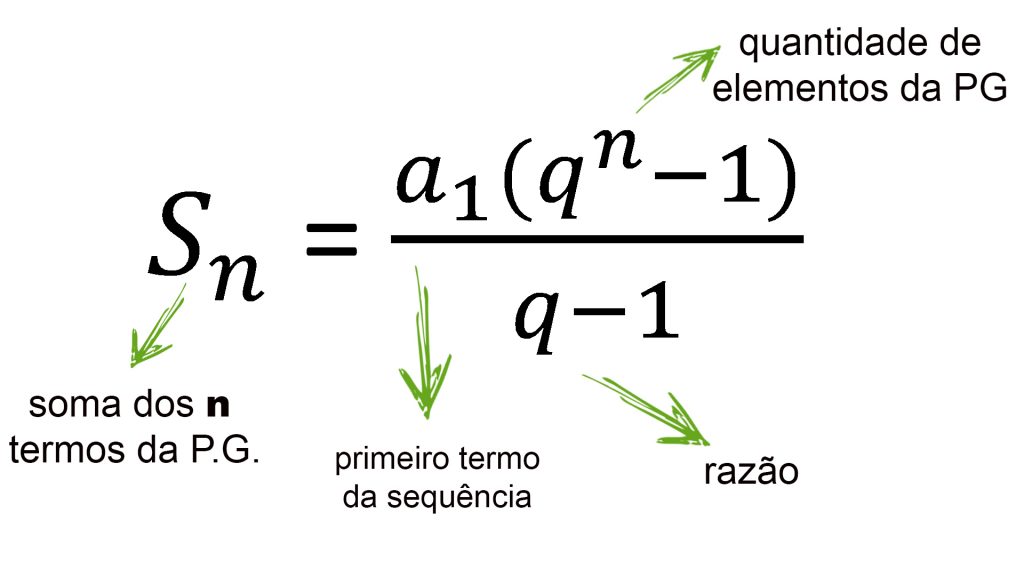
No caso da sequência acima, a1 = 1, q = 2, para N elementos. Então, fica S = 1*(2^N-1)/(2-1) = 2^N-1, que é a mesma conta.
Eu prefiro a prova visual…
Veja também:
Visualize a sequência de Fibonacci https://asgunzi.github.io/Fibonacci
Fórmula de soma de PA visual
https://ideiasesquecidas.com/2015/09/04/soma-visual-de-pa
Laboratório de Matemática
ideiasesquecidas.com 
Republicou isso em Forgotten Math.
CurtirCurtir