Terminei de ler Moby Dick, obra imortal de Herman Melville. Em outro post, escrevo alguns insights baseados no livro. Neste post, uma curiosidade. Na contra capa do livro, um quadrado curioso, cuja foto está colocada abaixo. Pergunta: o que é este quadrado? Obs. (Descobri que este símbolo é da Editora 34, e não do Moby …
Tag: Forgotten Math
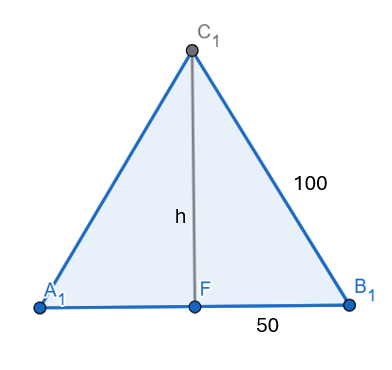
Resposta do puzzle da área da vaca
Enunciado O Sr. Smith tem uma área no formato de um triângulo equilátero, de lado 100m. Ele quer prender a sua vaquinha num dos lados do triângulo. A vaca terá uma corda, que limitará o máximo possível que ela pode alcançar dentro da propriedade. Qual o raio da corda, de modo que a área da …
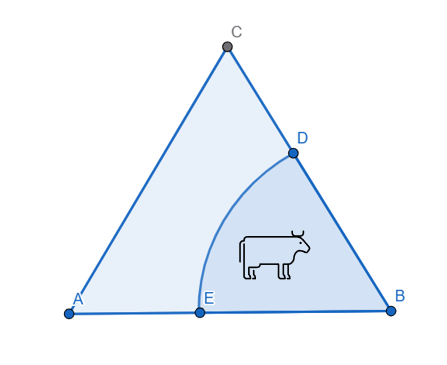
Puzzle da área da vaca
O Sr. Smith tem uma área no formato de um triângulo equilátero, de lado 100m. Ele quer prender a sua vaquinha num dos lados do triângulo. A vaca terá uma corda, que limitará o máximo possível que ela pode alcançar dentro da propriedade. Qual o raio da corda, de modo que a área da vaca …
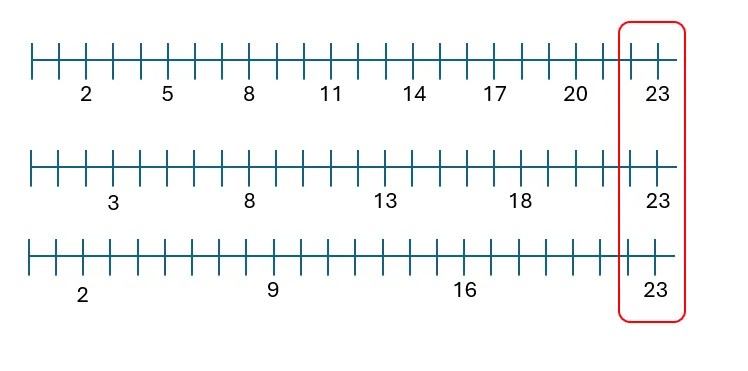
Resposta desafio das balas
O professor trouxe à turma uma quantidade de balas, porém, só distribuirá se eles conseguirem adivinhar o número de balas. Ele dá algumas dicas: Quando divido de três em três, sobram duas balas Quando divido de cinco em cinco, sobram três balas Quando divido de sete em sete, sobram duas balas Resposta: A forma mais …

Desafio das balas
O professor trouxe à turma uma quantidade de balas, porém, só distribuirá se eles conseguirem adivinhar o número de balas. Ele dá algumas dicas: Quando divido de três em três, sobram duas balas Quando divido de cinco em cinco, sobram três balas Quando divido de sete em sete, sobram duas balas Ajude a nossa turma …

Os Retângulos de Fibonacci
Os números de Fibonacci são aqueles em que o número seguinte é a soma dos dois anteriores: 1, 1, 2, 3, 5, 8, 13, 21, etc… A proporção áurea, ou o número de ouro, é um número que representa a proporção perfeita, e está ligada a belas formas. Há uma relação interessante entre os números …
Resposta probleminha de fatoração
Prove que $latex 2^{n}-1$ é composto para n composto. Exemplo. Para n = 9 (composto, 9 = 3*3): $latex 2^{9}-1 = 511 $ E 511 = 7*73, é composto. Resposta. Se n é composto, n= a*b $latex 2^{n} - 1 = 2^{ab} -1$ Dá para fatorar da seguinte forma: $latex 2^{ab} -1 = (2^{a} - …
Problema de fatoração
Prove que 2^n-1 é composto para n composto. Exemplo. Para n = 9 (composto, 9 = 3*3): 2^9-1 = 511 E 511 = 7*73, é composto. Minha resposta no post seguinte.

A Biblioteca de Babel de Borges
Sempre gostei muito de livros, livrarias, bibliotecas. Muito me fascinou a concentração de conhecimento da humanidade espalhada em tomos esquecidos por corredores inumeráveis. Hoje em dia, os livros físicos estão obsoletos, dando lugar à Internet e AI. O conto "A Biblioteca de Babel", do escritor argentino Jorge Luís Borges, é delicioso de ler, envolvendo livros, …
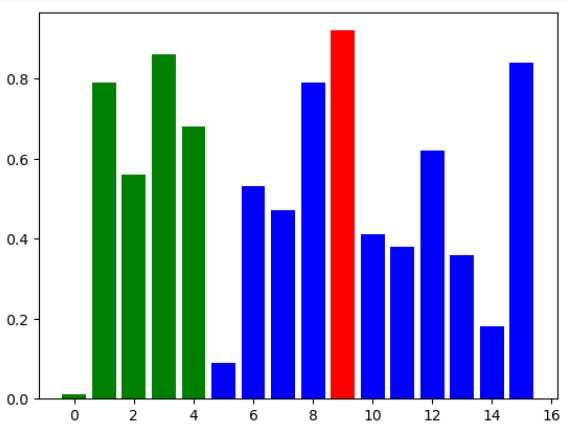
O problema da secretária – Solução
Formulação:Imagine que você está entrevistando candidatos para um emprego de secretária, e quer contratar o melhor possível. Há algumas regras adicionais, em relação a um processo comum: você só pode entrevistar um candidato por vez, deve tomar uma decisão imediatamente após a entrevista e não pode voltar atrás em uma decisão já tomada. Se rejeitar …

O problema da secretária Imagine que você está entrevistando candidatos para um emprego de secretária, e quer contratar o melhor possível. Há algumas regras adicionais, em relação a um processo comum: você só pode entrevistar um candidato por vez, deve tomar uma decisão imediatamente após a entrevista e não pode voltar atrás em uma decisão …

Resposta do puzzle das vacas e das galinhas
Em um sítio, o número de vacas é o triplo do número de galinhas.Somando as patas de todas as vacas e as patas de todas as galinhas, chega-se a um total de 280 patas. Quantas vacas e quantas galinhas há neste sítio? Poderíamos resolver via continha, x = vacas e y = galinhas. Mas, vamos …


Você precisa fazer login para comentar.