Pergunta: Dado um grid retangular formado quadrados unitários, com m linhas e n colunas, a diagonal principal passa por quantos quadrados?

Resposta simples: A diagonal passa por m + n – mdc(m,n) quadrados.

Resposta completa:

Imagine o que a diagonal faz com o grid: ela tem que percorrer igualmente as m linhas e as n colunas.

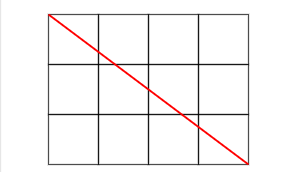
Neste grid de 3 linhas e 4 colunas, é como se a diagonal dividisse 4 por 3.

Ou seja, a resposta tem relação com divisão. No caso, 4/3 = 1 + 1/3. Ocupo 1 quadrado e 1/3 da primeira linha; depois 2/3 restantes e 2/3 da segunda linha, e 1/3 + 1 quadrado da terceira linha.

Ou seja, 2 quadrados em cada linha, dando 6 quadrados por onde passa a diagonal.

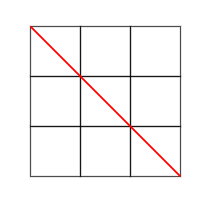
Agora, o curioso é quando coincide o mesmo número de linhas e colunas, porque aí a diagonal passa exatamente pelo vértice, e portanto, passa por menos quadrados.

Baseado nas observações acima, vamos deduzir a fórmula.

Suponha que estamos no quadrado 1 (no canto superior esquerdo). Para chegar ao final, devo atravessar n-1 “barreiras verticais”, e m – 1 “barreiras horizontais”. Toda vez que atravesso uma barreira dessas, passo para outro quadrado.

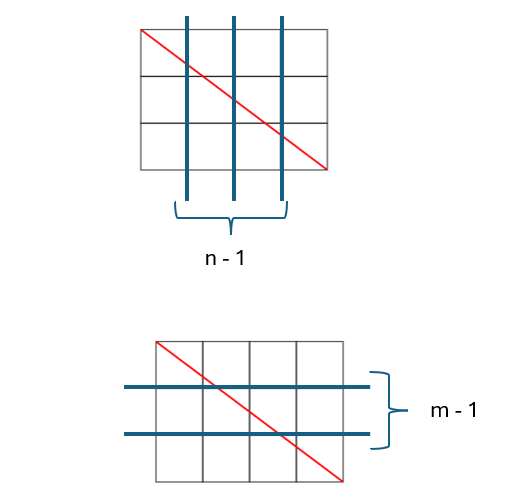
Portanto, no pior caso, vou passar por 1 + (n-1) + (m-1) quadrados.

Ou seja, já estou no primeiro quadrado, tenho que passar por n-1 verticais e m-1 horizontais.

Entretanto, há o caso em que a diagonal passa exatamente pelo vértice. E quando isso ocorre? Lembra acima, que comentamos que tem relação com divisão? Ocorre quando a divisão em linha é exatamente igual à divisão na coluna, ou seja, no mdc (máximo divisor comum) de ambos os números.

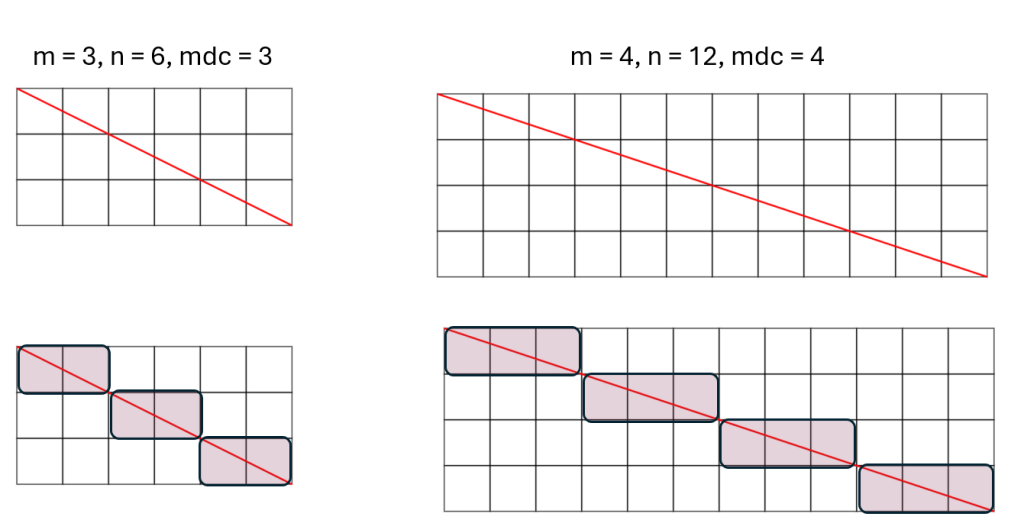
No primeiro exemplo acima, mdc = 3, o que divide as linhas em grupos de 1 e as colunas em grupos de 2. No final de cada bloco, há coincidência exata dos números inteiros, e a diagonal passa no vértice.

Quando há um bloco desses e a diagonal passa no vértice, podemos tirar uma unidade da fórmula original.

Há mdc(m,n) blocos, só que o último bloco não conta, porque não há grid à direita do último bloco. Então devemos descontar mdc(m,n) – 1 casos.

Colocando na fórmula:

quadrados = 1 + (n-1) + (m-1) – (mdc(m,n) -1)

Simplificando:

quadrados = n + m – mdc(m,n)

Ex 1. m = 3, n =4. mdc(3,4) = 1

quadrados = 3 + 4 -1 = 6

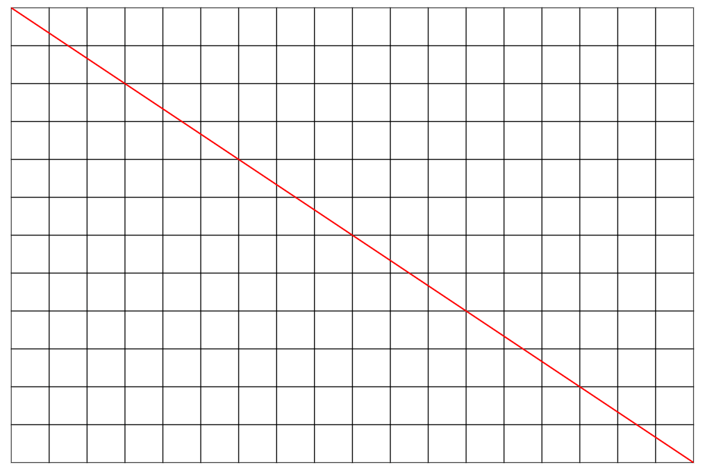
Ex 2. m = 4, n =12. mdc(4,12) = 4

quadrados = 4 + 12 – 4 = 12 (pode contar na figura acima).

Escrevi uma rotina para ajudar a desenhar o grid, confira no link a seguir: https://asgunzi.neocities.org/ArteMatematica/GridDiagonal