Enunciado

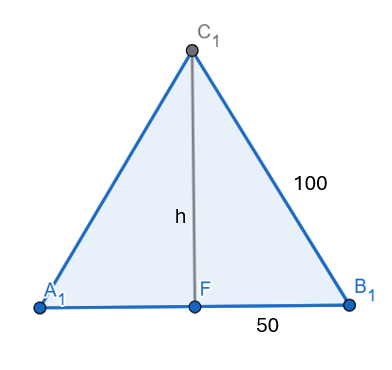
O Sr. Smith tem uma área no formato de um triângulo equilátero, de lado 100m.

Ele quer prender a sua vaquinha num dos lados do triângulo. A vaca terá uma corda, que limitará o máximo possível que ela pode alcançar dentro da propriedade.

Qual o raio da corda, de modo que a área da vaca seja exatamente igual à metade da área total do Sr. Smith?

Nota: A fonte do problema é um dos livros de matemática do Ian Stewart, só não lembro qual exatamente.

Solução

A área do triângulo é dada por A = 100*h/2, onde h é a altura do triângulo e 100 é o tamanho do lado.

Para achar a dimensão h, basta fazer a conta do triângulo de Pitágora para a metade do triângulo equilátero:

h^2 + 50^2 = 100^2

→ h^2 = 100^2 – 50^2

→ h = 86,6m

A área de um círculo é dada por pi*r^2. Não queremos saber a área de um círculo todo, queremos apenas 1/6 da área total, já que o triângulo equilátero que ângulos de 60o.

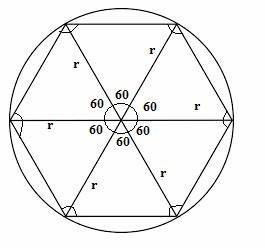
E também queremos que a área do setor circular seja metade da área do triângulo.

A área do setor circular dentro do triângulo é igual a pi*r^2/6

Portanto:

pi*r^2/6 = (100*h/2)/2

pi*r^2= 6*100*86,6/4

E isolando o r, temos

r= 64,3m

Portanto, a corda deve ter 64,3m.