Este é um clássico problema de “perseguição curva”.

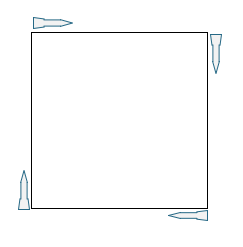
1. Os mísseis começam nos vértices de um quadrado e apontam inicialmente para o míssil à direita.
2. Cada míssil ajusta continuamente sua direção para seguir o alvo.
3. A trajetória dos mísseis será uma curva em espiral em direção ao centro do quadrado.
4. A distância entre os mísseis diminui constantemente.

Embora os mísseis estejam em movimento curvilíneo, a velocidade relativa entre eles permanece constante devido à simetria do problema.

Eu gosto de pensar assim. Imagine que você é um míssil e está vendo o seu alvo. Você ajusta continuamente sua rota, de modo que, para você, é uma linha reta.

Como todos eles farão o mesmo, é o mesmo que ter um quadrado, menor, só que rotacionado.

A distância a ser percorrida é distância inicial entre dois mísseis adjacentes: d=100 km.

A velocidade de aproximação relativa entre dois mísseis adjacentes é igual à v=50km/h.

Portanto, d/v = 100/50 = 2h

Os mísseis levarão 2 horas para se encontrarem no centro do quadrado.