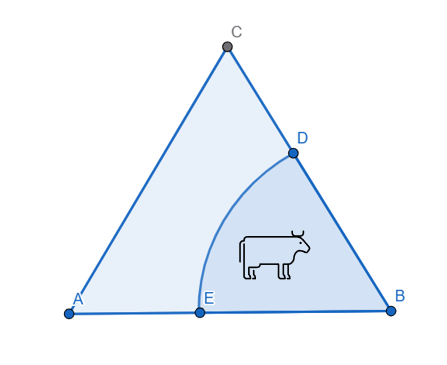
O Sr. Smith tem uma área no formato de um triângulo equilátero, de lado 100m. Ele quer prender a sua vaquinha num dos lados do triângulo. A vaca terá uma corda, que limitará o máximo possível que ela pode alcançar dentro da propriedade. Qual o raio da corda, de modo que a área da vaca …






Você precisa fazer login para comentar.