Pergunta.

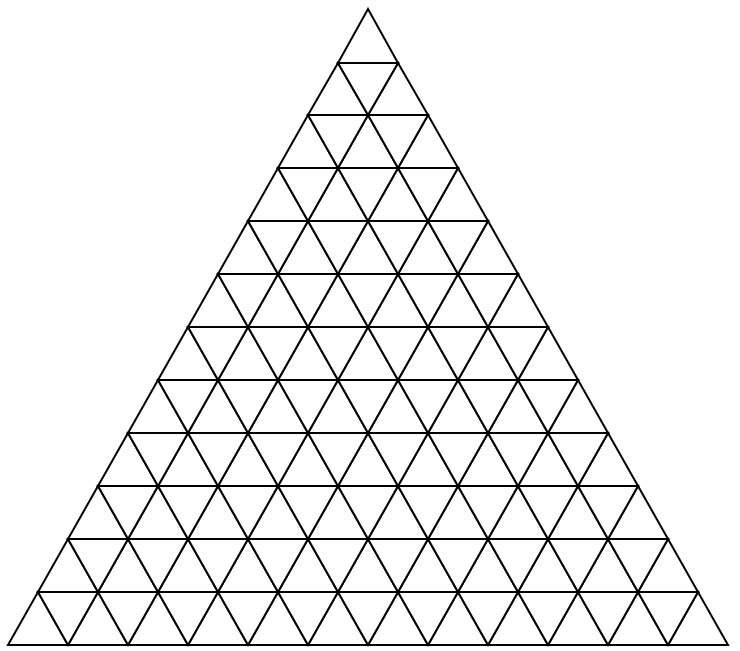
Seja um triângulo equilátero de lado n, formado por triângulos equiláteros de lado 1.

Quando há um triângulo equilátero pequeno que coincide com o centro do triângulo maior, o triângulo pequeno é removido.

Quando o centro do triângulo maior não coincidir com o centro de nenhum triângulo menor, nenhum triângulo é removido.

Nessas condições, é possível cobrir o triângulo equilátero restante com um trapézio formado por três triângulos equiláteros de lado 1, para N = 2^2026? 2^2027? 2^2028?

Inspirado na Revista Eureka!, no 20.

Resposta

Nota: demorei vários dias para resolver este exercício, e isso com o auxílio de computador para traçar os triângulos. Não é um problema fácil.

Passo 1: Contagem. Há quantos triângulos equiláteros menores?

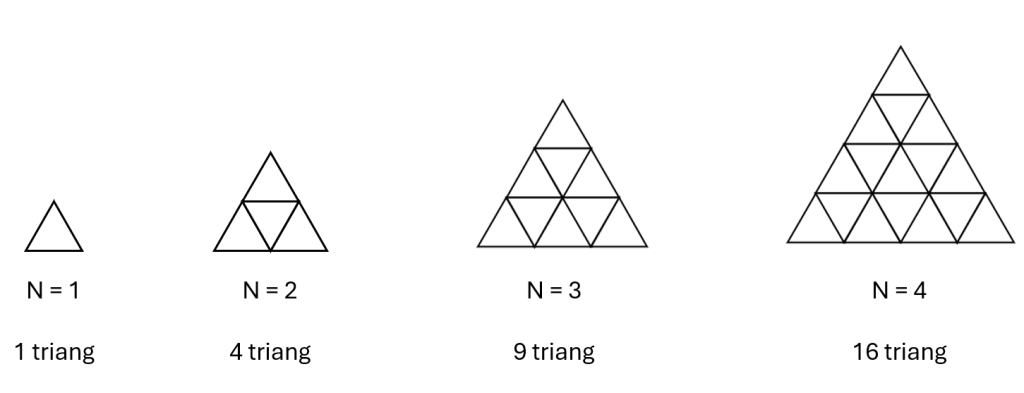
Há N^2 triângulos menores. Conte os casos acima, para ver.

Como provar isso? A cada linha nova, adiciono o mesmo valor da linha acima, mais dois triângulos. Dá uma soma do tipo 1 + 3 + 5 + 7 +…. Essa soma de ímpares dá um quadrado perfeito, e há uma prova muito bonita para isso.

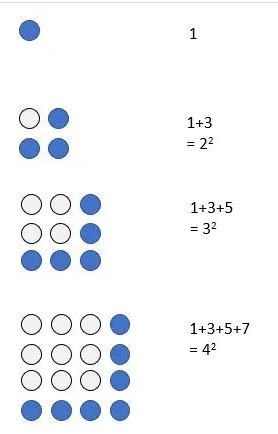
Passo 2: Em quais situações há triângulos removidos?

Agora, identificar quando temos triângulos removidos, e contar quantos sobram. Como um trapézio do problema tem 3 triângulos, se não for múltiplo de 3, não tem solução.

Fazendo alguns exemplo, um padrão fica claro. Para:

– N múltiplo de 3, não há triângulo menor removido

– N múltiplo de 3+1, o triângulo é para cima

– N múltiplo de 3+2, o triângulo é para baixo

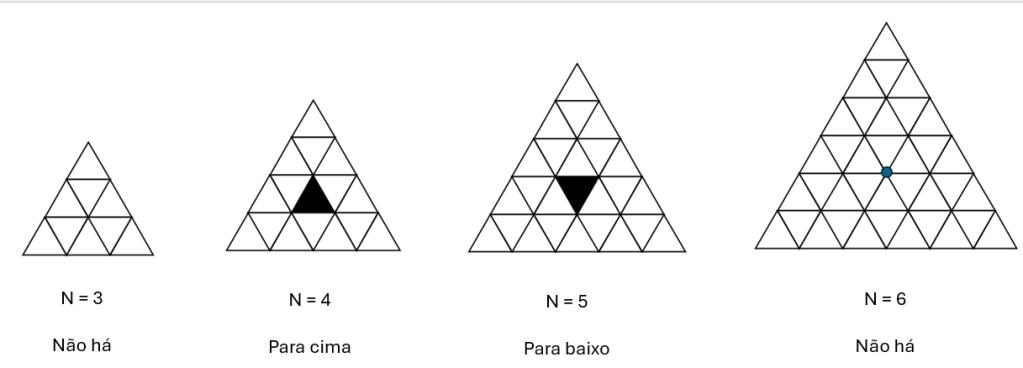
Uma forma de visualizar isso é pensar que, a cada N+1, uma linha de triângulos é adicionada, e o centro “desce” um pouco.

Fazendo a conta do número de triângulos exceto o central (quando tiver), vemos que sempre são múltiplos de 3, então este critério de contagem não elimina triângulo algum.

Uma prova mais algébrica:

N = 3k -> N^2- 0 (não desconta o central) = 9k^2 é múltiplo de 3

N = (3k + 1) -> N^2 – 1 (desconta o central) = 9k^2 + 6k +1 -1 = 9k^2 + 6k (é múltiplo de 3)

N = (3k + 2) -> N^2 – 1 (desconta o central) = 9k^2 + 12k +4 -1 = 9k^2 + 12k + 3 (é múltiplo de 3)

Passo 3: Colorir alguns exemplos

N <= 3: Não tem como colorir, porque o trapézio nem “cabe”.

N = 4: Não dá para colorir, falta espaço. Vide exemplo abaixo.

Para N =5, 6 e 7, é possível colorir tranquilamente (tudo feito no braço):

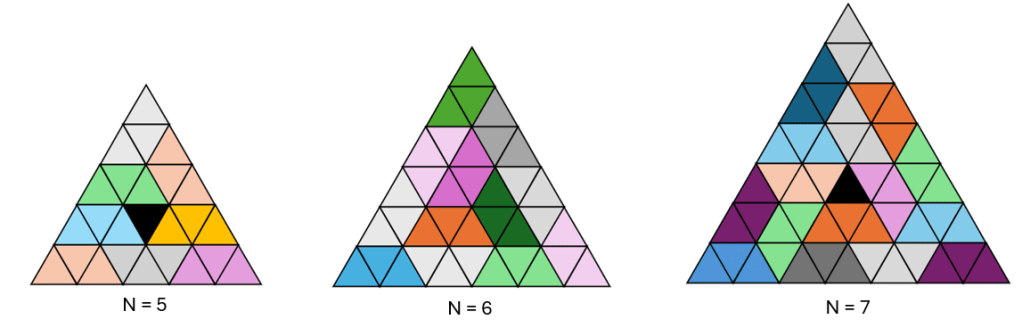
Note o caso N = 6, o quão fácil é. E o N = 7, bem mais complicado.

Para N = 8 também foi possível fazer. Isso leva a crer que é possível colorir para todos maiores do que 4.

Passo 4: Generalizar

Já vimos que tem um padrão, que se repete de 3 em 3: sem triângulo central a retirar, triângulo para cima, triângulo para baixo.

Vamos começar do caso mais fácil, sem triângulo central. Como pensar num padrão para aproveitar o que já temos? Depois de pensar por muito tempo, encontrei uma solução.

Passo 4.1: Sem triângulo central

O caso N = 6 tem solução (visto acima). O caso N = 9 é o próximo com características de centro igual. Este “envolve” o caso N = 6, e os ladrilhos cabem certinho.

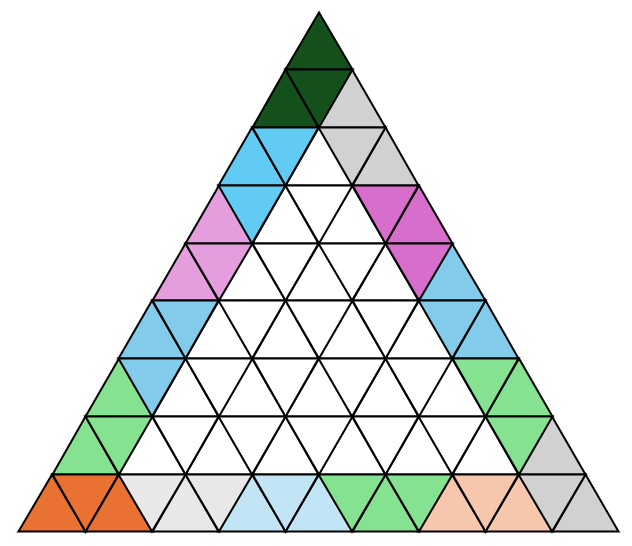
Imagine o trapézio como um Lego. Para N = 9, vamos usar o miolo igual a N = 6, e acrescentar um trapézio de 3 triângulos em cada lado a mais na envoltória. Para N = 12, mesma coisa, tomamos como base o N =9 resolvido. Assim, todos os N múltiplos de 3 (e maior igual a 6) têm solução.

Vamos usar lógica semelhante para os próximos casos. Uma coisa boa de olhar assim é que o centro retirado do triângulo vai ficar na posição correta ao adicionar a camada “externa”.

Passo 4.2: 3k +1

Para 3*k+1, temos solução para N = 7. Vejamos N=10.

Oh não, não dá certo como no caso anterior! O que fazer agora?

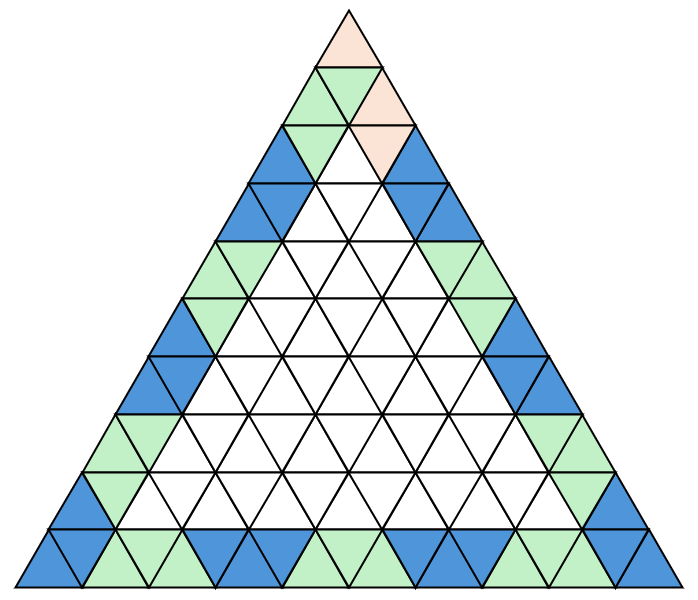
Uma coisa que fiz foi resolver o caso no braço, para tentar chegar à alguma conclusão. E sim, tem solução. Vide abaixo.

Portanto, para dar certo, é necessário “invadir” um pouco do triângulo interno e rearranjar o mesmo.

Qual o lado do triângulo interno a invadir para dar certo? O lado com 2 trapézios de orientação diferente, conforme figura do caso N =7.

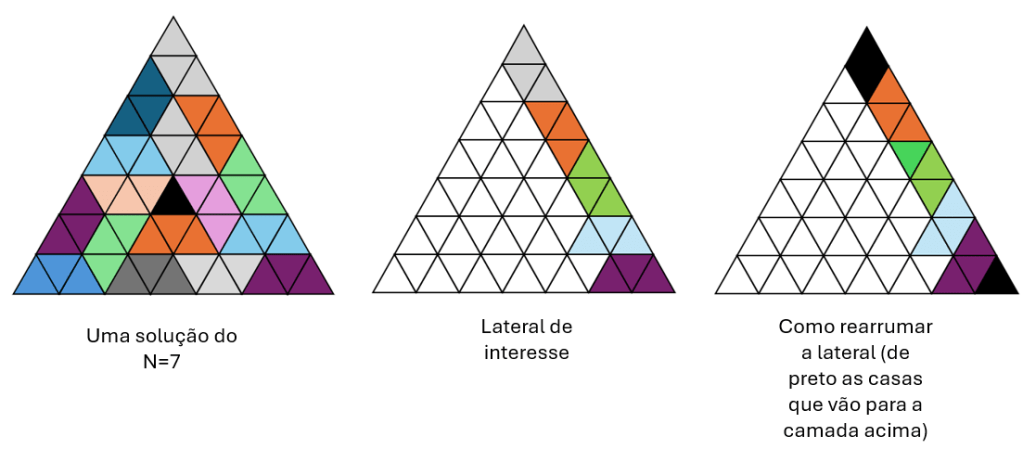
Note como é possível rearranjar os triângulos de modo a não afetar outras casas além das coloridas.

E sempre vai ter um lado com tais características, pelo algoritmo gerador mostrado acima.

Passo 4.3: Caso 3k+2

O caso 3k+2 é até mais fácil que o anterior. Vide para N = 11, por exemplo. São “invadidos” novamente três triângulos do lado interno, marcados com rosa. Porém, o lado que contém os triângulos invadidos somam 12, múltiplo de 3.

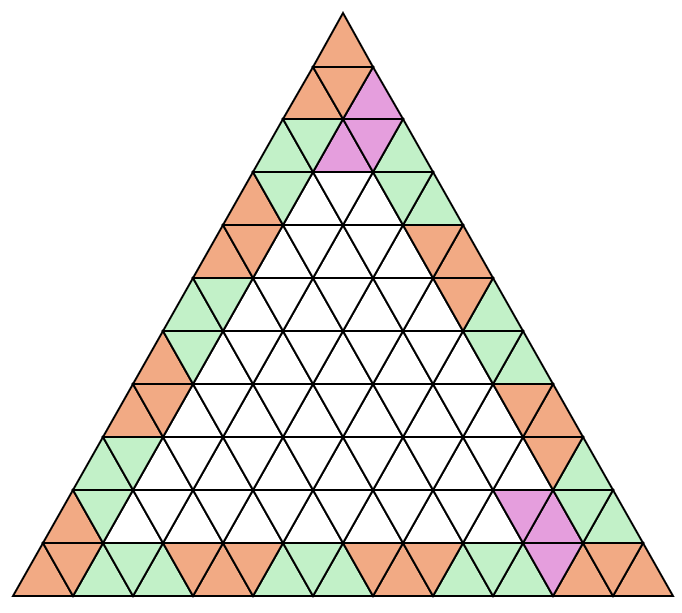
Então há um procedimento claro. Pegar um triângulo interno que tenha um dos lados preenchidos por trapézios.

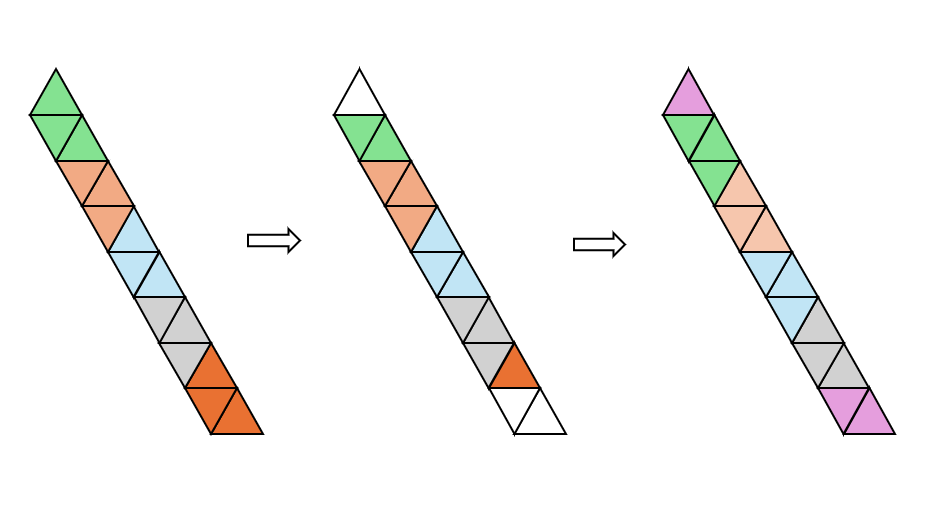
Tire um trapézio, e vire os demais encaixando. Aí vai ficar no formato desejado. E para os demais N = 3K+2, é o mesmo procedimento.

Conclusão

Portanto, para N >4, sempre há solução possível.

Resolvemos alguns casos simples, e mostramos como generalizar, inserindo camadas para cada um dos três casos onde o centro se posiciona. Por indução, é possível achar solução para qualquer N>4.

Deixei o código para gerar os triângulos no Github abaixo. Foi feito com shapes no Excel, utilizando VBA. Para colorir, foi no braço: selecionei o triângulo e pintei.

https://github.com/asgunzi/triangulos_equilateros

Sobre o chatGPT. Joguei o problema no chatGPT (versão free) e ele respondeu com generalizações completamente erradas. Fui dando dicas para ele corrigir os erros, mas foram muitas iterações.

Originalmente, é uma prova do tipo Olimpíada de Matemática. A menos que a pessoa saiba um pouco ou tenha uma capacidade muito grande, é bem difícil resolver a mesma com lápis e papel, no meio de outras questões, numa prova de algumas horas!