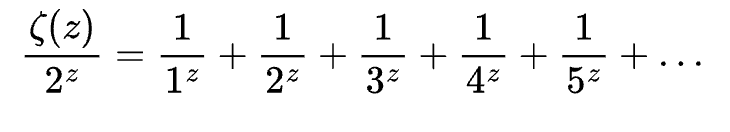A hipótese de Riemann é uma conjectura matemática complicada, que está profundamente relacionada à distribuição dos números primos. Há um prêmio de US$ 1 milhão para quem a resolver.

Neste texto, só queria fazer uma pequena relação entre primos e a série.

A função Zeta de Riemman é dada por:

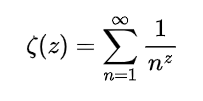
Onde a parte real de z é maior do que 1 (z pode ser complexo).

Mas qual a relação da função Zeta com números primos? Não parece nada direto…

Há uma forma bastante interessante de mostrar esta relação, que vi no livro “Prime Obsession”, de John Derbyshire. Vou resumir aqui.

Vamos expandir os termos para melhor visualização.

A primeira observação a fazer é a de que a série converge, para z>1. Não vou provar aqui, mas o livro acima fica como referência. A convergência é importante porque, senão, pode levar a resultados incorretos.

Se dividirmos todos os termos da fórmula por 2^z, teremos:

Ou seja, todos os números no denominador serão pares:

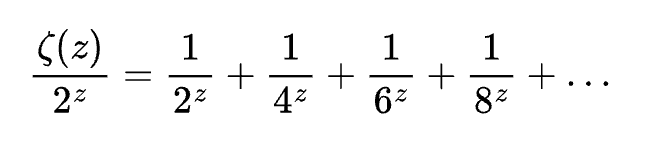
Subtraindo a série original desta última, temos:

Ou:

Note que é como se tivéssemos eliminado os pares.

Fazendo o mesmo, mas agora dividindo por 3ˆz:

E subtraindo da série anterior, vemos que os múltiplos de 3 foram eliminados.

O próximo número é o 5ˆz, que vai eliminar os múltiplos de 5 remanescentes. E note que 5 é primo, pois nenhum dos números anteriores o dividiram.

No final das contas, a série original pode ser representada por uma sequência envolvendo números primos:

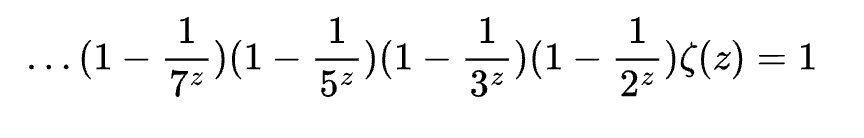
Daí, fica mais clara a relação entre a série original e números primos.

É uma lógica semelhante ao Crivo de Erastótenes, para identificar números primos.