Como medir o comprimento de algo muito pequeno?

Ora, pegue uma fita métrica, talvez um paquímetro, uma lupa, e meça.

Certo, mas e se for algo muito, muito pequeno mesmo? Um átomo, ou o núcleo de um átomo, ou menor ainda?

Ora, pegue um microscópio que aumenta 200x, meça o tamanho aumentado e faça a proporção para corrigir, algo assim.

Só que microscópios comuns têm limite.

O comprimento de onda da luz visível varia entre 400 e 700 nanômetros (nm). Não conseguimos enxergar algo menor do que isso. E átomos são da ordem de angstrom, que dá 0,1 nm.

É como se o comprimento de onda fosse a escala mínima da régua. Menor do que isso, temos que trocar a régua.

É, aí começa a ficar complicado. E se “trocássemos a régua”? Ao invés de usar luz visível, utilizar alguma onda eletromagnética com comprimento de onda menor? Como raios-X?

O problema é que não conseguimos enxergar os raios-X (só o Superman consegue, o que implica que ele é um ser radioativo).

O que conseguimos fazer, com raios-X, são medidas indiretas. Passar uma folha de ouro, digamos, nos raios-X, e depois revelar a chapa. Com isso, é possível contar o quanto de raios passaram pelo material e quantos não passaram. Trocando os materiais, testando outras potências, temos uma medida indireta do material – não é como o Superman, mas é o melhor que dá para fazer.

J. J. Trompson e outros pesquisadores fizeram experimentos semelhantes, com resultado curioso. A maioria dos raios atravessava a folha de ouro, mas uma porcentagem dos raios não atravessava.

Uma forma de modelar este problema é o seguinte. Imagine que o núcleo do átomo é uma bolinha com um certo diâmetro. Tenho a área da folha retangular, e a área dos núcleos dos átomos. Quando o raio-X bate no núcleo, ele não passa, por ser denso, e quando passa fora do núcleo, ele atravessa.

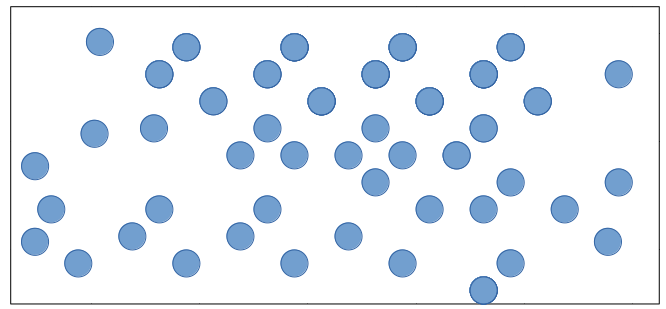
Podemos simplificar este caso para 2D, porque dificilmente um núcleo de um átomo vai ficar exatamente atrás de outro – por ser extremamente pequeno, e ainda mais quando mudamos parâmetros diversos e repetimos o experimento.

A quantidade da energia que não passa, dividida pela energia total dá uma noção da área do núcleo pela área do átomo, e assim conseguimos estimar o raio do núcleo.

Para uma comparação, o raio de um átomo é da ordem de 10^-10m, e o raio do núcleo é da ordem de 10^-15 m. A notação científica engana. Vejamos a diferença, 10^5 = 100.000. Se pegarmos 1 mm e multiplicarmos por 100.000, dá 100.000 mm = 100 metros. Ou seja, o núcleo é do tamanho de uma pulga, enquanto o átomo como um todo é do tamanho de um trem!

O que tem no resto do átomo, fora do núcleo? Os elétrons. Sejam como partículas ou ondas (que é discussão para outro dia).

Última pergunta: e para tamanhos menor ainda, como fazer?

Existe um limite para medir precisamente a posição e a velocidade de uma partícula, e este limite é dado pelo Princípio da Incerteza de Heisenberg.

Onde h é a constante de Planck.

Não dá para medir com precisão absoluta a posição e o momento (massa*velocidade) de uma partícula.

Uma explicação popular é que medir a posição envolve emitir um sinal (um fóton, digamos), que colide com o elemento a ser medido e depois é capturado por algum dispositivo. Se o elemento a ser medido for muito maior do que o fóton, zero problemas. Porém, se forem da mesma ordem de grandeza, a medição vai interferir no elemento a ser medido – é como se a régua mudasse o desenho que estou medindo.

Portanto, não é tão fácil assim medir o infinitamente pequeno.

(baseado no Feynman Lectures on Physics, mas com minhas palavras)