Resposta do Desafio: a corda e o arco

Em por Arnaldo Gunziem ForgottenMath, Matemática

Resposta do desafio apresentado anteriormente (link):

Tenho uma reta de tamanho 5000 m, por onde passam os trilhos de uma ferrovia.

Imagine que eu acrescente um metro à ela, resultando em 5001 m, porém eu mantenha os pontos iniciais e finais. A ferrovia agora será disposta num formato de um arco, conforme a figura abaixo.

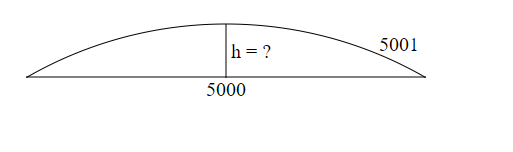
Pergunta: qual o valor da altura h?


Do arco:

\theta * r = 5001 \; (Eq. 1)


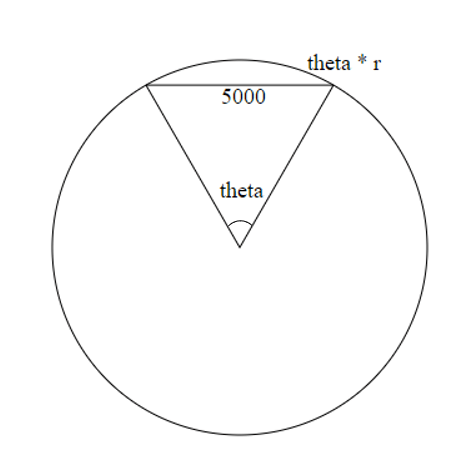
Da corda:

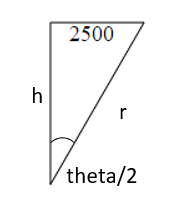
\sin (\theta/2) * 2500 /r \rightarrow r = \frac{2500}{\sin (\theta /2) } \; (Eq. 2)

Das equações (1) e (2), temos:

\frac{\theta * 2500 }{\sin (\theta/2)} = 5001


Ou seja:

\frac{\theta}{\sin ( \theta /2)} = 5001/2500 \approx 2,0004


Fazendo a conta no Excel:

\theta \approx 4^\circ \approx 0,06981 rad


Para encontrar o raio

\theta * r = 5001 \rightarrow r \approx 7163,05


Para encontrar o h:

\cos(\theta /2) = h/r \approx h = r * \cos(\theta/2) = 71590,41


Finalmente, a diferença é de:

r - h = 43,63 m

O que é bastante contra intuitivo, apenas um metro a mais causar essa diferença.

Veja também:

Lab. Matemática

Deixe um comentário