A Estatística tem um problema, o de que há muitos termos com nomes parecidos ou pouco explicativos.

O Desvio-padrão e Erro-padrão são casos assim.

Resumo rápido:

– Desvio-padrão: mostra o quanto os dados variam em relação à média
– Erro-padrão: mostra o quanto a média calculada varia em relação à média verdadeira da população

É confuso e provavelmente a descrição acima pouco ajudou, por isso, vamos detalhar a seguir.

— –

O desvio-padrão (σ ou s) é a medida mais conhecida de dispersão. Digamos que medimos a altura de uma série de pessoas e temos uma lista.

import numpy as np
alturas = [168, 164, 183, 166, 166, 156, 165, 193, 172, 177, 170, 176, 172, 176, 191, 176, 181, 163, 173, 153, 175, 167, 162, 175, 171, 161, 177, 161, 170, 168, 174, 168, 158, 171, 151, 163, 165, 198, 175, 171, 146, 179, 169, 163, 162, 166, 176, 177, 139, 172]

O desvio-padrão mede o quanto as alturas se espalham em torno da média.
Se o valor for grande, significa que as pessoas têm alturas bem diferentes; se for pequeno, as alturas são mais parecidas.

Este pode ser calculado com um comando como np.std(alturas).

(Um detalhe é que há uma diferença entre desvio-padrão populacional e amostral. Como os dados acima são amostras da população total, e não a população total, temos que inserir um fatorzinho de correção, ddof=1. Quer dizer que perdemos um grau de liberdade. Isso porque o cálculo do desvio-padrão depende da média, e como a média também é gerada a partir da amostra, perdemos um grau de liberdade.)

# Número de elementos
n = len(alturas)
# Desvio-padrão amostral
desvio_padrao = np.std(alturas, ddof=1)
# Erro-padrão da média
erro_padrao = desvio_padrao / np.sqrt(n)
print(f"Média das alturas: {media:.1f} cm")
print(f"Desvio-padrão amostral: {desvio_padrao:.1f} cm")
print(f"Erro-padrão da média: {erro_padrao:.1f} cm")

Resultado:

Média das alturas: 169.4 cm
Desvio-padrão amostral: 10.6 cm
Erro-padrão da média: 1.5 cm

Para ver o desvio-padrão, uma forma é plotar um histograma e pensar na dispersão dos dados obtidos. Quanto maior o desvio, mais dispersos estão os dados.

— –

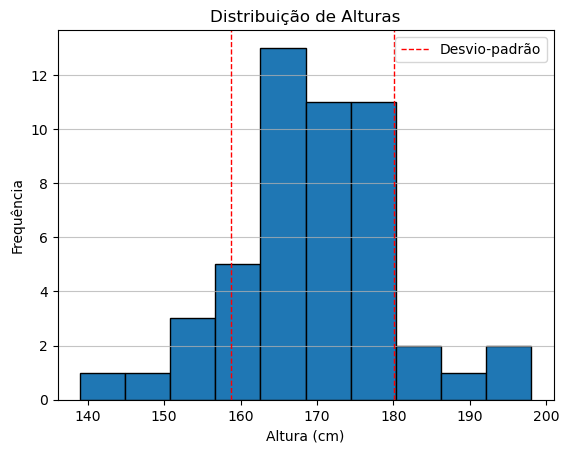
Já o erro-padrão mede a precisão da média.

Imagine que eu tire a média da lista acima. O quanto esta média varia em relação à média populacional real? A noção é a de que quanto mais dados eu tenho, mais certeza tenho de que a média calculada vai ser próxima da real.

A fórmula é simples:

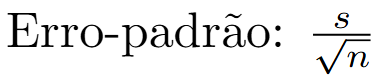
onde:
– s = desvio-padrão da amostra
– n = número de observações

Em Python:

n = len(alturas)
erro_padrao = desvio_padrao / np.sqrt(n)

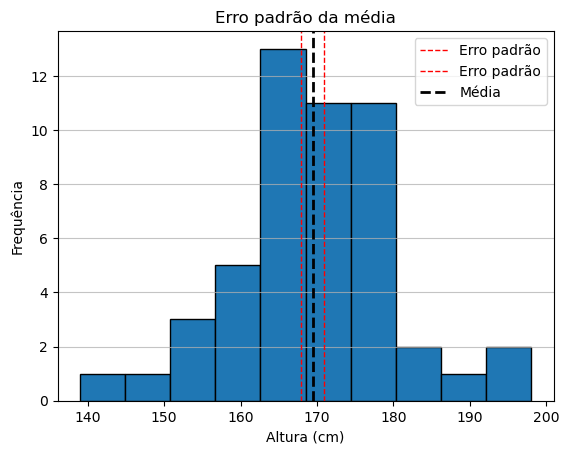
Se, ao invés de 50 dados tivéssemos 100, e mesmo valor de s = 10.6, o erro-padrão seria de 1.06 cm ao invés de 1.5 cm (ou seja, ganharíamos mais certeza de que a nossa média de 169.4 cm está correta).

Em resumo:

Desvio-padrão: dispersão dos dados,
Erro-padrão: precisão da estimativa da média (ou de outro estimador).

Pense no desvio-padrão como o quanto cada pessoa é diferente das outras.
Pense no erro-padrão como o quanto a média que você calculou pode estar diferente da média verdadeira da população.