Seja um triângulo equilátero de lado n, formado por triângulos equiláteros de lado 1.

Quando há um triângulo equilátero pequeno que coincide com o centro do triângulo maior, o triângulo pequeno é removido.

Quando o centro do triângulo maior não coincidir com o centro de nenhum triângulo menor, nenhum triângulo é removido.

Nessas condições, é possível cobrir o triângulo equilátero restante com um trapézio formado por três triângulos equiláteros de lado 1, para N = 2^2026? 2^2027? 2^2028?

Ex. Para N = 5, temos a seguinte situação, tirando o triângulo em preto.

Ex. Para N = 6, o centro coincide com a posição da bolinha. Como não coincide com o centro de nenhum triângulo menor, nenhum é removido.

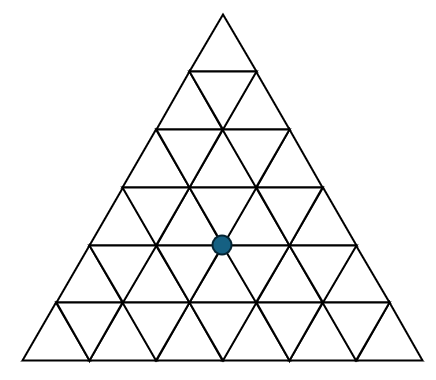
E um trapézio é como o da figura.

Consegue preencher com trapézios?

Resposta no próximo post.

Nota: Este desafio é um pouco mais difícil do que a média postada aqui. A inspiração é a revista Eureka n. 20, que contém problemas de olimpíadas de matemática.