Tarefa: Crie um vetor com 23 números aleatórios de 1 a 365 (representando o dia do ano em que cada uma das 23 pessoas fazem aniversário). A seguir, verifique se há dois números iguais nesta lista (ou seja, se pelo menos duas pessoas em 23 fazem aniversário no mesmo dia).

O código a seguir faz exatamente como o enunciado, ordenando para melhor visualização, e checando onde há repetições.

import random

N = 23

aniversarios = [random.randint(1, 365) for _ in range(N)]

aniversarios.sort()
print(aniversarios)

for i in range(N-1):
if aniversarios[i]==aniversarios[i+1]:
print(“Repetição no dia: “, aniversarios[i])
break

Resultado:

[ 9, 9, 14, 39, 52, 73, 97, 138, 140, 142, 157, 164, 186, 207, 217, 250, 259, 273, 293, 313, 320, 348, 359]

Repetição no dia: 9

Outra rodada (desta vez, não há repetição).

[16, 34, 70, 83, 86, 87, 92, 96, 106, 113, 158, 174, 205, 219, 242, 249, 258, 266, 273, 309, 358, 361, 364]

Dá para fazer similar no Excel. Basta usar a fórmula para gerar um aleatório entre 1 e 365, para 23 linhas, e colocar uma formatação condicional para destacar repetidos.

=ALEATÓRIOENTRE(1;365)

No caso abaixo, duas pessoas fazem aniversário no dia 347 do ano.

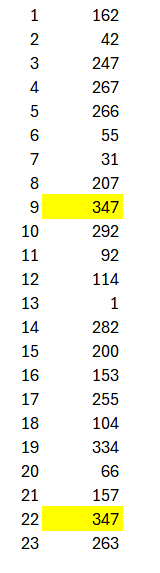
Deixei os códigos no github: https://github.com/asgunzi/paradoxo-aniversario

E como calculamos analiticamente a chance de pelo menos duas pessoas fazerem aniversário no mesmo dia?

Vamos imaginar que há duas pessoas.

Suponha que a pessoa 1 faça aniversário em algum dia do ano.

A probabilidade da pessoa 2 fazer aniversário no mesmo dia é de 1/365.

A probabilidade da pessoa 2 NÃO fazer aniversário no mesmo dia da pessoa 1 é o complemento, 364/365. Tipo, se eu faço aniversário no dia 17/jan, outra pessoa deve fazer aniversário em qualquer dia, menos 17/jan, para não coincidir.

Com 3 pessoas, esta terceira deve fazer aniversário em dias diferentes da primeira e da segunda. A chance de todos aniversários serem em dias diferentes é (364/365)*(363/365).

Vamos incrementando o número de pessoas.

Para 4 pessoas, (364/365)*(363/365)*(362/365)

E assim sucessivamente.

Lembre-se de que esta probabilidade é a de todos fazerem aniversário em dias distintos. O que queremos é o complemento, ou seja, a chance de que pelo menos duas pessoas façam aniversário no mesmo dia. Ou seja, 1 – (364/365)*(363/365)*(362/365)…

Ou, como diria Charlie Munger, “Inverta, sempre inverta”.

Dá para fazer com calculadora, mas como é uma conta chatinha, vamos escrever um pequeno código.

produto = 1
for i in range(1,N):
produto *= (365-i)/365

resultado = 1-produto

print(resultado)

Para N = 23, dá 50,72% de chance de pelo menos duas pessoas no grupo fazerem aniversário.

Para N = 70, dá 99,91%.

Rode os códigos algumas vezes, para se convencer deste aparente paradoxo!