Há algumas formas simples de pensar e visualizar métricas de erro como MAE, MSE, e a relação disso com mediana e média.

Quem trabalha com machine learning, estatística e afins, já ouviu falar dos termos MAE (Mean Absolute Error) e o MSE (Mean Square Error). Vamos ver uma forma de interpretar ambos em relação às conhecidas mediana e média da Estatística descritiva.

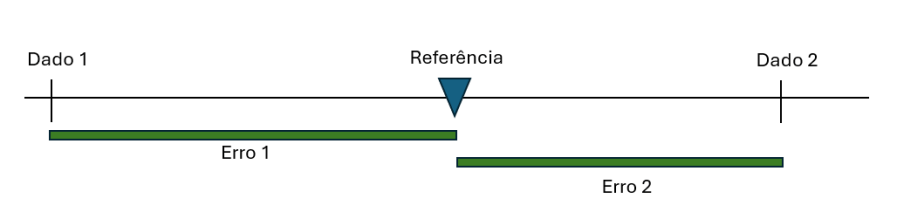
Vamos pensar em uma dimensão: uma lista de itens, que na reta dos números, seria algo assim:

Agora, imagine um único ponto de referência, em relação ao qual será medido o erro. O ponto de referência pode estar em qualquer lugar.

O erro é a distância entre o ponto de referência e os dados.

E o erro normalmente é medido como o erro absoluto (o comprimento da barrinha) ou o erro quadrático (o comprimento ao quadrado). Há outras métricas possíveis de erro, como o erro máximo, mas vamos nos ater aos citados.

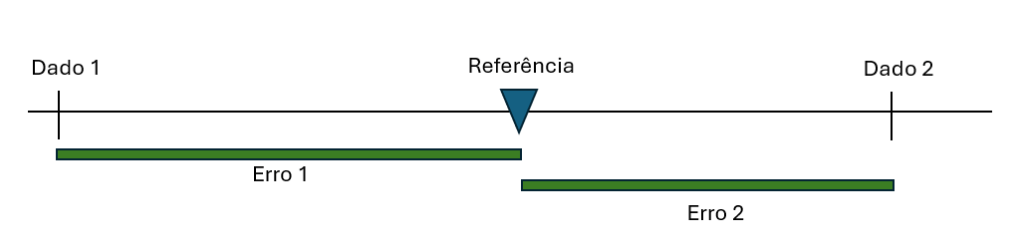
Qual o melhor lugar para o ponto de referência ficar, de modo a minimizar o erro?

Intuitivamente, o melhor lugar é em algum ponto central em relação aos dados, porque quanto mais longe desses, maior o erro.

No diagrama a seguir, note que as barrinhas de erro são muito maiores do que no diagrama anterior.

Agora, o melhor local exato depende de qual métrica estamos utilizando, se é o erro absoluto, quadrático ou algum outro.

Olhando para o erro absoluto

Vamos agora argumentar que, quando estamos olhando para o erro absoluto, o ponto que minimiza o erro é a mediana da série.

A mediana é aquele ponto que divide a distribuição exatamente ao meio: ordene os seus dados, e pegue aquele dado que esteja exatamente acima de 50% e abaixo de 50% dos valores.

O erro absoluto dos dados em relação a mediana vai ter um valor.

Agora, vamos pegar um ponto de referência um pouquinho maior que a mediana. Ponto de referência = a mediana mais um delta. O que acontece com o erro?

Em relação ao erro calculado anteriormente, todos os pontos à esquerda vão ser acrescidos de um delta erro. E todos os pontos à direita vão ter o erro decrescido de um delta erro. Em outras palavras, o erro vai aumentar para quem está à esquerda, porque o ponto de referência se afastou um pouco; e o erro vai diminuir para quem está à direita, porque o ponto de referência chegou mais perto deles.

Como a mediana está exatamente no meio, vamos ter o erro à esquerda maior do que o erro à direita. No diagrama, a mediana está em laranja, e temos um acréscimo de delta erro em relação a 4 pontos à esquerda, e diminuição de delta erro em 3 pontos à direita.

Todos os valores de delta erro terão a mesma magnitude, porque o movimento do ponto de referência afeta igualmente a todos.

Se fizer a mesma coisa, porém com o ponto de referência menor que a mediana, vamos ter o oposto, o erro à direita maior do que o erro à esquerda.

No diagrama, a mediana está em laranja, e temos um decréscimo de delta erro em relação a 3 pontos à esquerda, e acréscimo de delta erro em 4 pontos à direita.

Portanto, a mediana é o ponto ótimo, quando considerado o erro absoluto.

Para complementar, se o número de pontos for par, a mediana vai estar entre os pontos centrais.

E aí, um ponto de referência próximo à mediana, porém ainda entre os pontos centrais, vai ter igual efeito de deltas somando e decrescendo, dando efeito nulo no final.

Entretanto, se sair da faixa entre pontos centrais, cai no caso mostrado anteriormente.

E considerando o erro quadrático?

Considerando o erro quadrático, este será o quadrado do erro absoluto, e isso tem o efeito de que os pontos mais distantes terão maior contribuição.

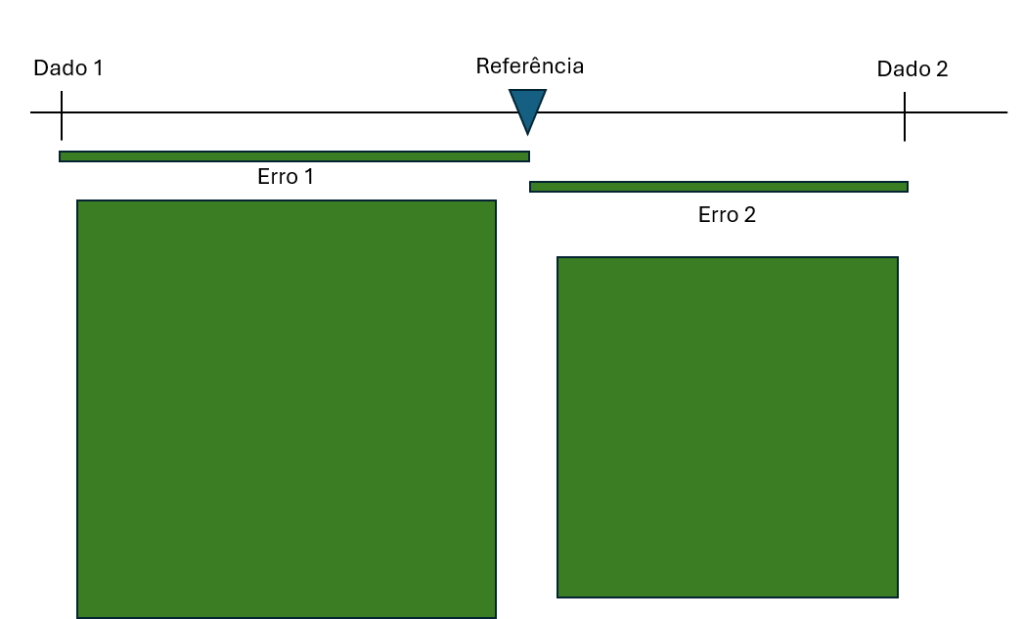
(Obs. O diagrama é ilustrativo, não está em escala)

O ponto que minimiza o erro quadrático é a média.

A forma mais simples de provar isso é com Cálculo. Seja uma função que calcule o erro em função do ponto de referência.

Vamos utilizar o velho truque de derivar e igualar a zero para encontrar o ponto mínimo.

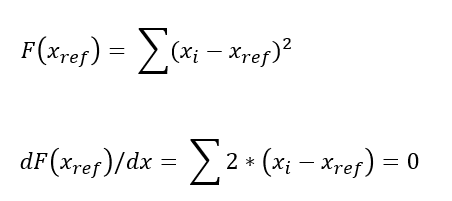
A derivada de x^2 é igual a 2*x. Fazendo isso para todos os fatores, temos:

Que é exatamente a definição da média.

E é por isso que os matemáticos gostam tanto do MSE, porque é fácil utilizar os poderosos truques de Cálculo e derivar soluções.

Para o erro absoluto, até dá para usar Cálculo, só que é mais complicado. Quando calculando o erro absoluto, a derivada é um “se”: se o valor dentro for maior do que zero, é a expressão, senão é o negativo dela. Isso complica bastante a conta – imagine fazer isso em N valores absolutos, teria uma árvore imensa de possibilidades.

Conclusões

Em resumo, a solução do MAE (Mean Absolute Error) é a mediana, e a solução do MSE (Mean Square Error) é a média. O RMSE (Root of Mean Square Error) é a raiz quadrado do MSE, e é útil para que a unidade de medida seja a unidade do valor estudado, e não o valor ao quadrado como o caso do MSE.

A mediana é menos sensível a outliers, enquanto a média é muito mais sensível (afinal, eleva a diferença ao quadrado).

Qual utilizar no dia-a-dia? É legal calcular ambas, porque há informações diferentes sendo transmitidas por esses indicadores.

Baseado em conversa com o amigo Ernée Kozyreff Filho.