Respostas dos desafios do último post.

1) Mostre que, dados três números inteiros distintos, sempre posso escolher dois tal que a soma seja par.
Exemplos: Dados 1, 4, 7, posso escolher 1 + 7 = 8, que é par. De 2, 3, 8, posso escolher 2 + 8 = 10, que é par.
Resp: Um número pode ser par ou ímpar – ou seja, ter resto 0 ou 1 quando dividido por 2.
Sejam p, q, r os números.
A soma de dois pares é par. A soma de dois ímpares é par também.
Se eu tiver dois números, posso pegar um par e um ímpar, aí a soma será ímpar. Como são três números, é a situação do princípio da casa dos pombos, o terceiro ou será par ou ímpar, e aí consigo pegar e somar dois pares ou dois ímpares para resultar num número par.
2) Mostre que, em qualquer conjunto de 10 pontos interiores a um quadrado cujos lados medem 3 unidades, há dois pontos cuja distância é menor ou igual a raiz de 2.
Exemplo de 10 pontos aleatórios.

Resp:
Imagine colocar 4 pontos o mais distantes possíveis dentro do quadrado. Esses serão muito próximos ao 4 vértices. Seja o raio igual à raiz de 2, que dá por volta de 1,41. Se qualquer outro ponto estiver dentro do raio, já temos a condição descrita no enunciado.

A figura não está exatamente em escala, mas dá para notar que sobra um pouquinho. 3 – 2*1,41 = 0,18. Suficiente para colocar mais um ponto, em cada um dos 4 “vãos”.
Pintando de vermelho, fica mais ou menos como na figura.
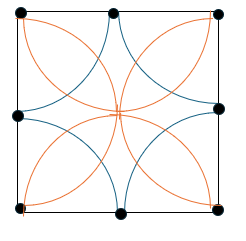
Bem no meio, sobra espaço para mais um pontinho, somando 9.

Se tenho 10 pontos, não há espaço para colocar o décimo a menos de raiz de 2 de qualquer um dos demais pontos. Portanto, pelo princípio da casa dos pombos, com 10 pontos necessariamente dois deles terão distância menor do que raiz de 2 entre eles.
3) Dados 3 inteiros distintos, sempre é possível escolher dois entre ele, digamos a e b, tais que é um múltiplo de 10.
Exemplo: 1, 4, 8.
Se a = 4 e b = 1,
Resp: É uma situação semelhante ao exercício 1. Porém, ao invés de pensar módulo 2, vamos pensar módulo 5.
Note que podemos reescrever a equação de forma amigável.
Ou seja, a equação é igual a:
Também notar que 10 = 2*5, ou seja, queremos pegar um múltiplo de 2 e um múltiplo de 5.
O fator 2 não é problema. Dados dois números a e b, se um deles for par, o produto ab(a-b)(a+b) será par.
Se a e b forem ímpares, (a+b) e (a-b) serão pares.
Portanto, nosso problema real é a equação ser múltiplo de 5.
Todo número inteiro, ao ser dividido por 5, terá resto 0, 1, 2, 3 ou 4.
Se um dos 3 números tiver resto 0, ou seja, por exatamente divisível por 5, problema resolvido. Escolhemos esse número para a.
Se um dos números tiver resto 1 e o outro tiver resto 4,
também problema resolvido, porque a soma dos restos dará 5 (ou seja, zero módulo 5).
Se um dos números tiver resto 2 e o outro tiver resto 3, também problema resolvido, porque a soma dos restos dará 5 (ou seja, zero módulo 5).
Se dois números tiverem restos iguais, também, sem problemas, porque a diferença dos restos dará 0.

Portanto, dos 5 restos possíveis, o 0 sozinho resolve o problema, dois restos iguais também, e as combinações 1-4 e 2-3, idem. Com três números, dois deles vão cair em algum desses casos. Não tem jeito, não tem casa suficientes para acomodar todos os pombos. CQD.
Até a próxima.
