Regressão logística – Domine esta técnica poderosa

A regressão logística é uma adaptação da famosa regressão linear, para os casos em que precisamos prever uma categoria de saída ao invés de um número. Ela utiliza uma função logística para modelar o resultado de uma variável dependente binária a partir de uma (ou mais) variáveis independentes.

E o que seria uma categoria? Uma categoria é uma saída não numérica. Por exemplo, “Sim” ou “Não”, “Aprovado” ou “Reprovado”.

Vamos ilustrar o uso da regressão logística a partir de um exemplo didático, que tem uma saída binária e apenas uma variável independente.

Suponha que trabalhamos numa loja de roupas, e tenhamos o histórico de clientes que fizeram compra ou não fizeram. Também, só para efeito de ilustração, vamos supor que saibamos a renda das pessoas que passaram pela loja.

O estado “Comprou?” é representado por 1, e o estado “Não comprou”, por 0.

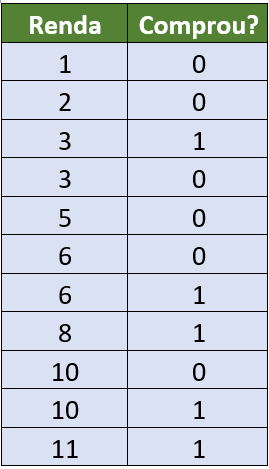
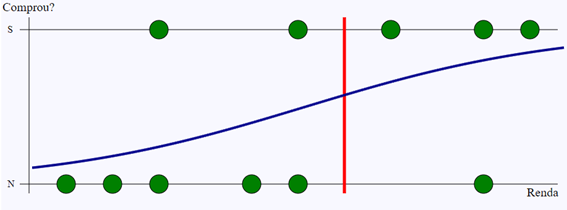
Podemos visualizar esse histórico de dados utilizando um gráfico como o seguinte, onde a Renda está plotada no eixo X, e as bolinhas representam se o cliente em questão comprou ou não.

Qual a probabilidade de o cliente comprar, dada como variável a faixa de renda?

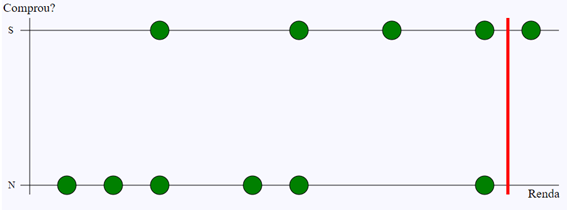
Uma forma extremamente simples de criar um modelo é utilizando um “se”: se acima de um valor de Renda, considero que ele compra. Abaixo deste valor, ele não compra. A linha vermelha abaixo indica o ponto de corte considerado.

Note que este patamar pode ser colocado em níveis diferentes, e o efeito será um modelo mais agressivo ou conservador.

Porém, o “se” citado tem um problema: ele não é diferenciável. Matemáticos em geral gostam de funções diferenciáveis, porque uma função derivável no domínio todo da função torna mais simples provar teoremas, encontrar mínimos etc.
Conseguimos imaginar uma função que tenha as propriedades desejadas?

Começar em zero e terminar em 1
Seja derivável em todos os pontos (ou seja, contínua, bem comportada)

Felizmente, temos uma função assim. É a função logística, dada por:

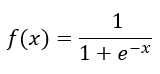
O formato da função é uma curva em S, começando em 0 e terminando em 1.

A função logística é monotônica crescente, com o jeitão dado acima. O seu resultado pode ser considerado uma porcentagem. No caso do exemplo, seria a probabilidade de fechar a compra, dada a renda do cliente.

De forma mais precisa, e analogamente à regressão linear, queremos encontrar coeficientes a e b na equação logística, que melhor fitem os pontos dados.

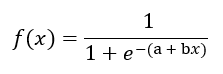
Podemos fazer uma pequena rotina no R, para encontrar os coeficientes exatos da regressão logística.

dados <- data.frame(Renda = c(1, 2, 3, 3, 5, 6, 6, 8, 10, 10, 11), Comprou = c(0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1))

fit <- glm(Comprou ~ Renda, data = dados, family = binomial)

Resultando em:

Comentando linha a linha. O dataframe dados conterá duas colunas, a da Renda e se Comprou – onde 0 significa “não” e 1 significa “sim”.

dados <- data.frame(Renda = c(1, 2, 3, 3, 5, 6, 6, 8, 10, 10, 11), Comprou = c(0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1))

A função glm, no R, faz a regressão logística. Na função, indico que a variável dependente é o Comprou, e a independente é a Renda.


fit <- glm(Comprou ~ Renda, data = dados, family = binomial)

O resultado é:

(Intercept) = -2.1280

Renda =0.3227

Ou seja, a equação que calcula a probabilidade do cliente comprar é:

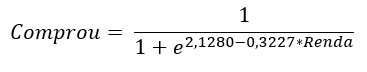
Por exemplo, inserindo Renda = 1 na equação, o resultado será 0,1412, ou seja, por este modelo, a probabilidade de um cliente de Renda = 1 efetuar a compra é de 14,12%.

Atualizando a tabela original, temos os seguintes valores.

Podemos visualizar a curva da regressão logística no mesmo gráfico.

Há casos em que saber a probabilidade é suficiente para a questão. Porém, há casos em que necessitamos de uma resposta binária, ao invés de probabilística: afinal, vai vender ou não?

Uma forma de usar a função logística para tal é considerar um limiar. Se a probabilidade estiver acima de uma determinada probabilidade, vamos considerar “sim”, senão, considerar “não”.

Por exemplo, este é o gráfico considerando a probabilidade acima de 0,55.

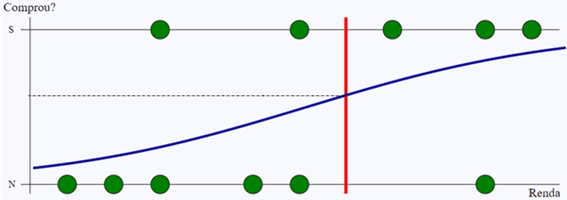
Outra pergunta vem deste método. Qual o limiar a considerar? Um limiar de certeza muito alto (ou muito baixo) não vai trazer ação útil alguma, como ilustrado no exemplo a seguir. A informação será óbvia: quem tem mais renda tem mais chance de comprar.

Para o modelo servir para tomada de decisão útil, ele tem que estar no limiar ótimo entre certeza e incerteza, algo que faz sentido, mas não é óbvio. Como podemos fazer isso?

Primeiro, vamos sumarizar o resultado obtido, em termos de previsão do modelo x histórico real de dados.

Os verdadeiros positivos são os que foram detectados pelo modelo, e pelo histórico eram mesmo positivos. A imagem abaixo destaca o verdadeiro positivo do exemplo.

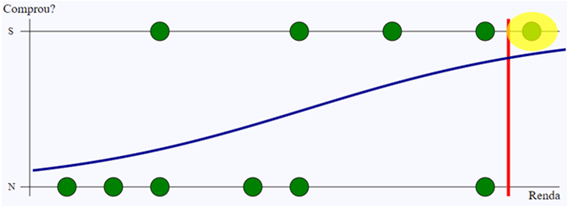
Os falsos positivos são os que o modelo classificou como positivo, mas não o são pelo histórico. No caso do exemplo, não houve nenhum, mas eles ficariam na região sublinhada em amarelo.

Os verdadeiros negativos são os que o modelo classificou como negativo, e que também o são no histórico de dados.

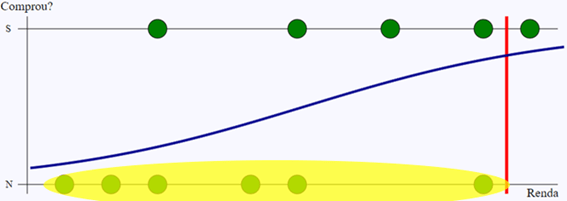
Já os falsos negativos são os que o modelo classificou como negativo, mas foram positivos no histórico.

Podemos fazer uma tabela para sumarizar os 4 casos descritos acima.

Há dois tipos de erros que podemos cometer: ter falsos positivos demais, ou falsos negativos demais. Em geral, ser muito criterioso em um dos lados implica aumentar os erros do outro lado, de forma que devemos equilibrar esses dois erros.

Para ajudar na avaliação da solução, a teoria Estatística apresenta algumas métricas boas.

Acurácia – Soma dos elementos da diagonal principal / Soma de todos os elementos. Interpretação: um número que indica o quanto o modelo acertou.
Para o caso do exemplo acima.

Sensititividade – De todas as observações da classe “Boa”, quantas o algoritmo classificou como “Boa”? São os verdadeiros positivos corretamente identificados.

Para o exemplo dado:

Especificidade – De todas as observações da classe “Ruim”, quantas o algoritmo classificou como “Ruim”? São os verdadeiros negativos corretamente identificados.

Para o caso do exemplo:

Em resumo:

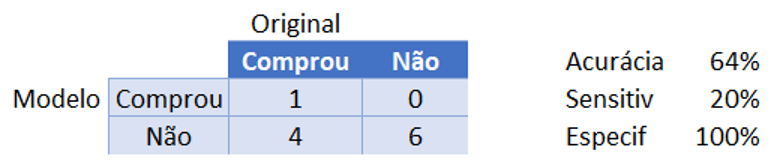
Embora o modelo tenha grande especificidade, não tem boa sensitividade.

Vamos verificar o modelo com um outro limiar de decisão, como o da figura abaixo. Até visualmente, é mais claro que é um limiar em que há mais equilíbrio entre os tipos de erros.

Para o novo limiar dado, temos as seguintes métricas:

E as métricas mostram que há maior equilíbrio entre sensitividade e especificidade, além de que a acurácia é maior.

Sugestão: refazer as contas acima.

Obs. O tipo de erro que vou priorizar depende do problema real em questão. Há casos em que o modelo deve minimizar fortemente falsos positivos, outros em que ele deve minimizar fortemente falsos negativos, e outros em que deverá haver um equilíbrio entre ambos. Não há como dizer de antemão. A Estatística dá as ferramentas, e o usuário deve saber como aplicar.

O caso mostrado foi de apenas uma variável. A utilização da técnica para o caso multivariado é análoga: ao invés de mensurar apenas o intercepto e um coeficiente angular, no caso multivariado haveria um coeficiente angular para cada variável independente. Felizmente, pacotes computacionais como o R já têm funções prontas que ajudam a fazer essas contas.
Aplicações. A regressão logística é uma ferramenta poderosa que pode ser usada em uma variedade de aplicações, incluindo: