A curva de Bézier é uma curva bastante elegante, formada a partir de um número de retas e com aplicações surpreendentes.
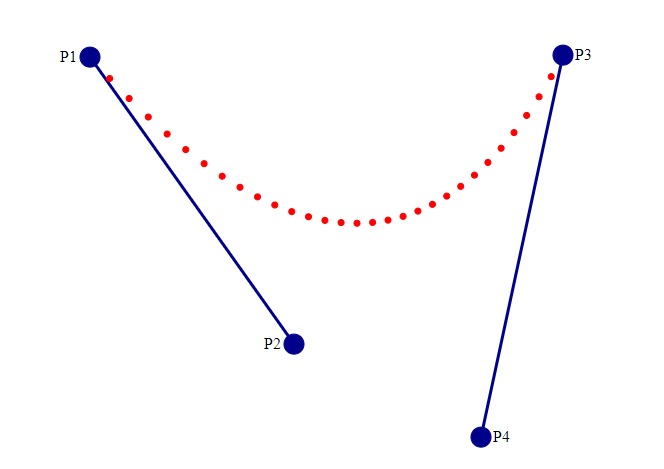
Ela foi criada pelo francês Pierre Bézier, funcionário da Renault, nos anos 1960 – chama a atenção também a data, relativamente muito recente para uma construção matemática simples.
Fiz uma versão interativa em Javascript D3, para mexer e sentir como ela funciona, disponível em:
https://asgunzi.neocities.org/ArteMatematica/Bezier01
Alguns prints abaixo:
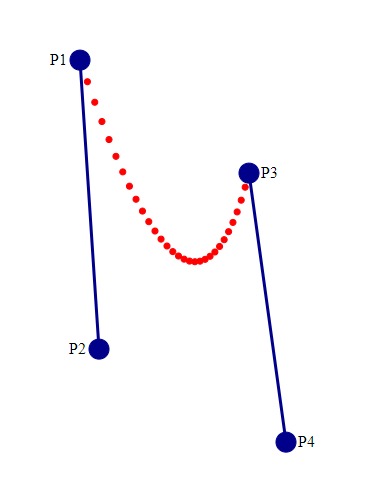
Basta arrastar qualquer dos pontos que formam as retas, para criar uma nova curva.

Como traçar a curva?
Vou explicar aqui a curva quadrática.
Pegue duas retas e divida em p pedaços.

Una o p-ésimo pedaço do primeiro com o p-ésimo pedaço do segundo (do final para o começo), usando uma reta.

Divida essa última reta em p pedaços também, e marque o p-ésimo pedaço.
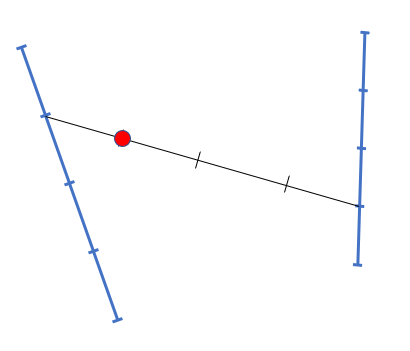
Repita o procedimento até o fim, e teremos a nossa curva.
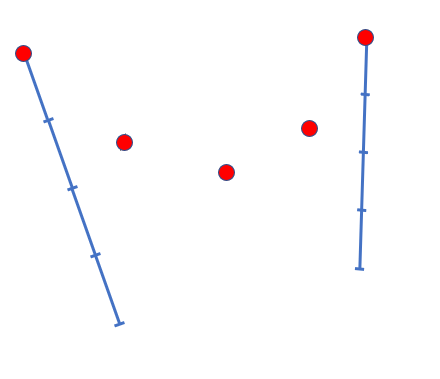
No caso com duas retas, teremos uma curva quadrática. É possível fazer procedimento similar com mais retas – se forem três, teremos uma cúbica, por exemplo.
E para que serve?
Bézier desenvolveu a curva para auxiliar o design de carros da Renault, a fim de tornar as curvas mais elegantes. Ou seja, dá para dizer que, desde Bézier, a curva ajuda a fazer o projeto de carros da Renault.

Foto da fonte a seguir.
https://www.bricsys.com/pt-br/blog/the-bezier-curve-how-car-design-influenced-cad
A técnica da curva de Bézier foi incorporada em sistemas CAD diversos, por ser uma curva suave contida no “convex hull” das retas, ou seja, no contorno de uma área dada pelas retas.
Nada mau para uma construção matemática simples!
Próximas rotinas a serem feitas são a curva de Bézier cúbica e de ordens superiores. Estão na lista de tarefas!
A rotina foi feita em parceria com o amigo Ernée Kozyreff Filho.
Veja também:
