Pequeno experimento, baseado no Andar do Bêbado (Random Walk).

Um bêbado começa do ponto (0,0), e anda aleatoriamente um passo para direita ou esquerda no eixo X, e para cima ou para baixo no eixo Y.

O percurso percorrido tem a aparência a seguir, e já fiz experimentos anteriores a respeito. Vide https://ideiasesquecidas.com/2024/06/26/pequeno-exercicio-sobre-random-walk/.

O experimento aqui é um pouquinho diferente? Depois de N passos, onde o bêbado para?

A ideia é baseada num comentário de Richard Hamming:

• Se você andar aleatoriamente como um bêbado, você vai parar em algum lugar num raio de raiz(N) passos da onde começou
• Se você tiver um objetivo e andar em direção a este, mesmo bêbado, vai ter percorrido próximo a N (imagine o mesmo bêbado caminhando em direção à uma moça muito bonita)

Bom, vamos ao experimento.

Vamos fazer o bêbado andar 500 passos, em duas dimensões, e guardar a posição final em que ele parou. Faremos isso muitas vezes, e vamos encontrar a média e o desvio padrão.

import random
import numpy as np

trials = 4000
passos = 500

posicao_final = []

for _ in range(trials):
posicao_x = 0
posicao_y = 0
for _ in range(passos):
passo_x = 1 if random.random() < 0.5 else -1
passo_y = 1 if random.random() < 0.5 else -1
posicao_x += passo_x
posicao_y += passo_y
posicao_final.append((posicao_x, posicao_y))

Calcular a média e o desvio padrão

media_x = sum(x[0] for x in posicao_final) / trials
media_y = sum(x[1] for x in posicao_final) / trials
media = (media_x, media_y)

rms = np.sqrt(np.mean([x[0]2 + x[1]2 for x in posicao_final]))
print(media, rms)

Resultado:

(-0.310, 0.301) 31.42

O resultado teórico é que a média é zero, e desvio padrão raiz(N)*p, onde p é o tamanho do passo.

Como o bêbado anda uma unidade no eixo X e uma no eixo Y, na diagonal o tamanho do passo dele é raiz(2).

Se foram 500 passos, então raiz(2*500) = 31.62 passos, bate com o resultado prático.

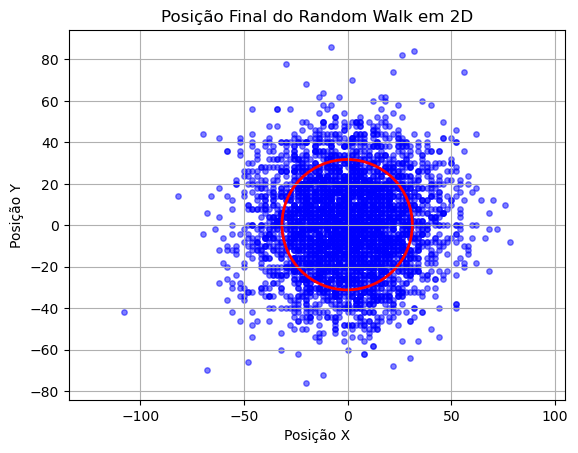
Vamos plotar as posições num gráfico, para ver como fica. O círculo vermelho é o raio do desvio padrão, ou seja, a maior parte do tempo, o bêbado vai parar dentro deste círculo.

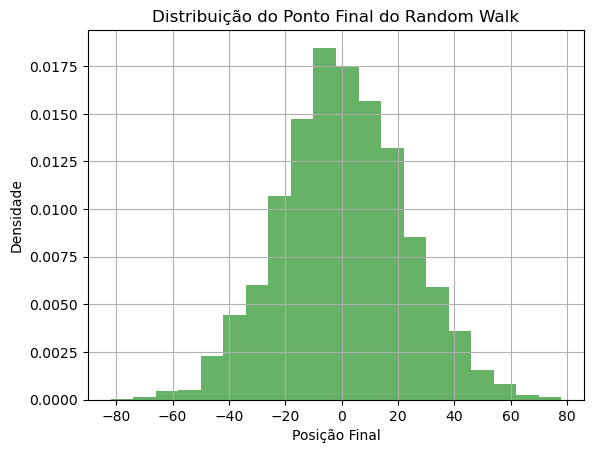
Outra forma de ver é olhando para o histograma da posição final. Neste caso, estou pegando apenas a dimensão X.

Random walks foram bastante estudados, e alguns resultados firmes são:

• Em uma dimensão (1D) e duas dimensões (2D): Um random walk SEMPRE retorna à origem (média das posições zero).

• Em mais dimensões (3D, 4D, etc.): A probabilidade de retorno à origem não é garantida e, na verdade, diminui com o aumento da dimensão. Em 3D, há 34% do bêbado voltar para casa, e 66% de chance dele se perder para sempre.

Uma interpretação intuitiva é que, quanto mais dimensões, mais fácil o bêbado se perder, por ele ter mais possibilidades de caminhos.

Portanto, Hamming estava certo ao afirmar que o bêbado não vai muito longe ao andar aleatoriamente.

Mesmo com aleatoriedades, o fato de ter um objetivo e não andar para qualquer lado já significa que você vai muito mais longe!

Código no Github: https://github.com/asgunzi/Andar_bebado_raio

Obs. Pequenos detalhes teóricos.

No cálculo de desvio padrão abaixo, considero que a média é zero.

rms = np.sqrt(np.mean([x[0]2 + x[1]2 for x in posicao_final]))

Além disso, a minha primeira abordagem estava ligeiramente errada, e é bom pontuar a diferença.

Eu estava calculando a distância para a origem em cada trial, e calculando o desvio padrão, como abaixo:

distancia_final = [np.sqrt(x[0]** 2 + x[1] ** 2) for x in posicao_final]
desvio_padrao = np.std(distancia_final)

Parece a mesma coisa, mas a diferença é que eu estava calculando a raiz em cada passo e depois calculando o desvio. O resultado teórico é relativo à distância RMS (Root Mean Square Distance), que é exatamente à da fórmula correta.