Conecte todos os pontos a seguir com arestas simples, de modo a minimizar a distância total de arestas.

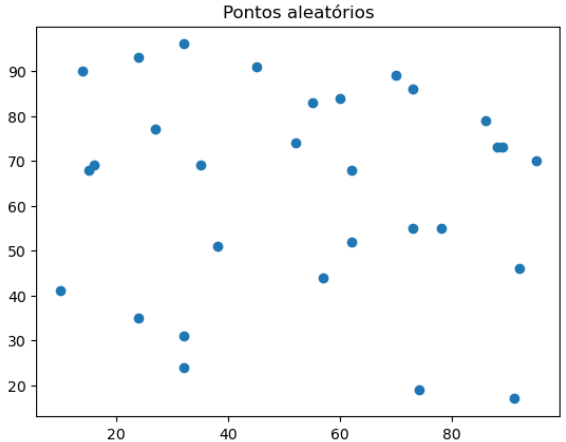
Dado um grafo, uma árvore geradora mínima (minimum spanning tree) é uma estrutura como a da figura a seguir, que também é uma solução possível para o problema acima.

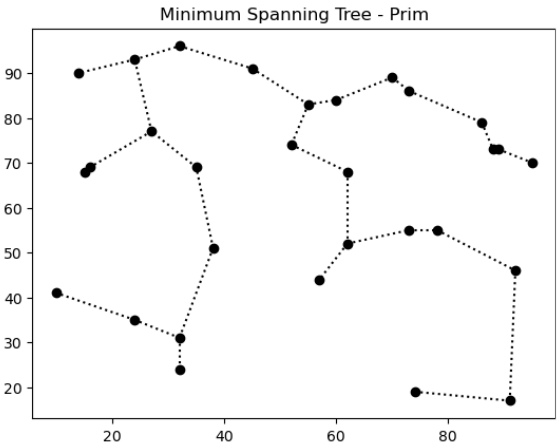
Ou seja, uma árvore que conecta todos os pontos da menor forma possível, em termos de distância percorrida pelos ramos. Outro exemplo aleatório abaixo.

Existem vários algoritmos que geram árvores assim. Uma bem simples é o algoritmo de Prim.

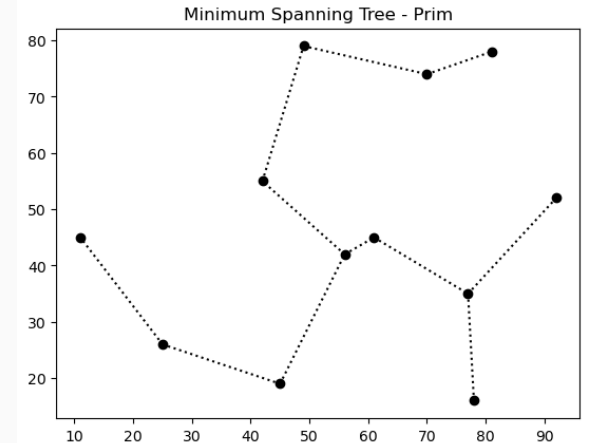
Em pseudo-código:

1. Inicializar:
   a. Selecionar um vértice inicial e adicioná-lo ao conjunto de vértices da árvore.
   b. Inicializar uma lista para guardar as arestas
2. Repetir até que todos os vértices estejam na árvore:
   a. Encontre a menor aresta que conecta um vértice dentro da árvore a um vértice fora da árvore.
   b. Adicione a menor aresta encontrada
   c. Adicione o vértice conectado ao conjunto de vértices da árvore.

Fiz um código para o algoritmo de Prim. Vide no Github: https://github.com/asgunzi/prim

Uma coisa legal é que podemos ver o resultado do algoritmo de forma simples.

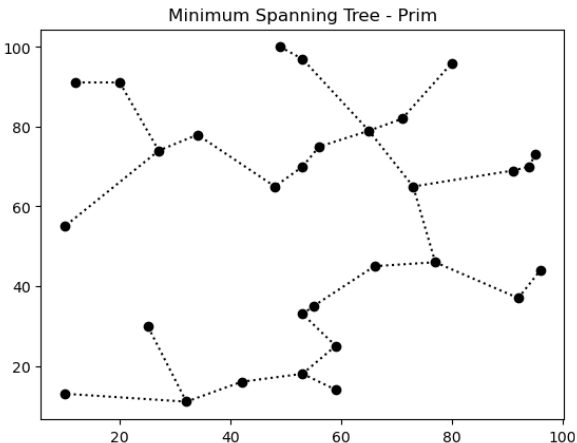
Aplicação: Qualquer problema que envolva encontrar caminho mínimo e a resposta na forma de árvore, ou seja, conectando pontos existentes, seja útil. Um problema clássico, o do caixeiro-viajante, tem uma solução aproximada, o algoritmo de Christophides, que utiliza como base um minimum spanning tree.

Curiosidade: No filme “Gênio indomável”, um dos problemas envolve árvores geradoras.

Vide:
https://www.cantorsparadise.org/the-math-problems-from-good-will-hunting-w-solutions/