Há dezenas de provas do Teorema de Pitágoras. Dezenas mesmo, basta procurar um pouco na internet.

Tem uma que conheço, bem bonita, e visual.

Vamos partir de um triângulo retângulo, de catetos a, b e hipotenusa c.

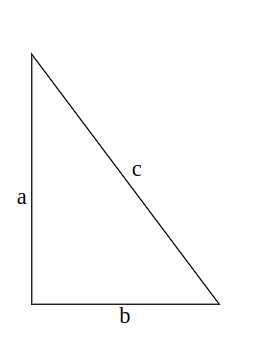
Segundo o teorema, a² + b² = c², o famoso “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

Vamos colocar 4 desses triângulos retângulos, iguais, formando um quadrado maior.

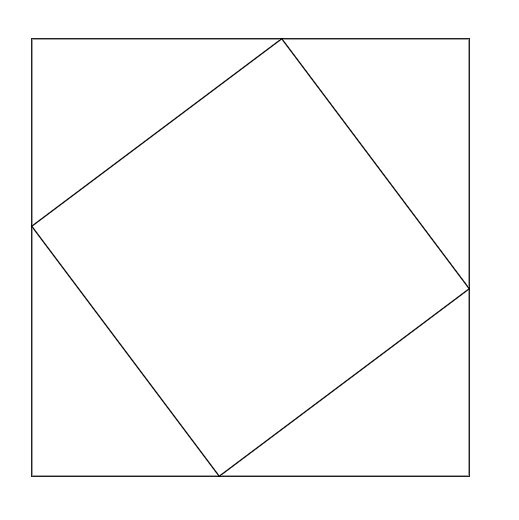
A mesma figura, mas com os rótulos indicando as dimensões.

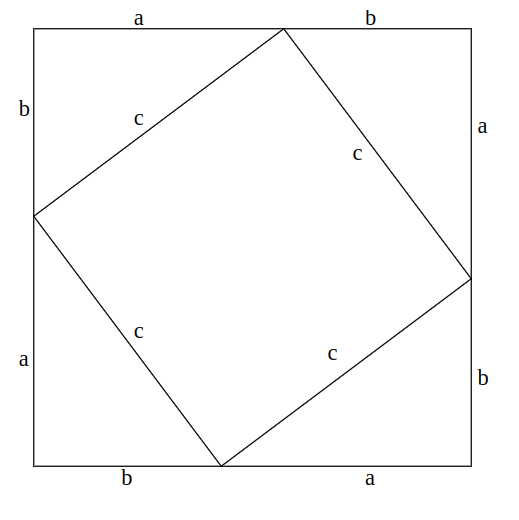
Temos que os triângulos formam um quadrado maior, de lado (a+b).

A área do quadrado maior é igual a (a+b)².

A área de um triângulo retângulo é ab/2. Como há 4 desses, as áreas dos 4 triângulos é igual a 4*ab/2 = 2ab.

Já o quadrado menor, do meio, tem lado c e área c².

Portanto, igualando a área do quadrado maior com os seus componentes:

(a+b)² = 2ab + c²

Desenvolvendo o binômio:

a² + 2ab + b² = 2ab + c²

Portanto,

a² + b² = c²

Só tem uma questão adicional relevante. Como eu sei que a área do meio forma um quadrado, e não um losango?

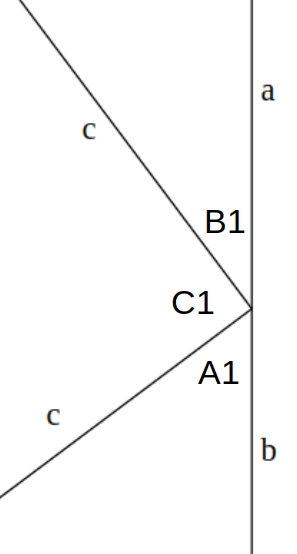
Ora, é só verificar que o ângulo B1 + C1 + A1 formam 180 graus (é uma linha reta). Mas B1 + C1 = 90 graus, porque são os mesmos ângulos internos do triângulo retângulo. Assim sendo, o ângulo C1 tem 90 graus.

Sendo assim, está provado o Teorema de Pitágoras!

Nota: Fiz um código para desenhar o triângulo, usando JS D3. Segue link no Github para o código:
https://github.com/asgunzi/Pit-goras/tree/main