Visualizando números Felizes e Infelizes

Os números felizes são um tópico divertido da matemática!

Vamos explorar algumas visualizações e códigos de apoio.

Para identificar um número é feliz, o procedimento é:

Iniciar com qualquer número positivo;
Substituir o número pela soma dos quadrados de seus dígitos: Por exemplo, se começarmos com o número 19, calculamos 1² + 9² = 1 + 81 = 82
Repetir o processo até que o número seja igual a 1 ou até que entre em um ciclo que não inclui 1

Se o número se transforma em 1, então ele é considerado um número feliz. Se o número entra em um ciclo infinito que não inclui 1, ele não é feliz. Ou seja, é um número triste:

Por exemplo, vamos ver se o número 19 é feliz:

1² + 9² = 1 + 81 = 82
8² + 2² = 64 + 4 = 68
6² + 8² = 36 + 64 = 100
1² + 0² + 0² = 1 + 0 + 0 = 1
Uma vez que chegamos a 1, podemos concluir que 19 é um número feliz.

Outro exemplo, o número 4 não é um número feliz:

4² = 16
1² + 6² = 1 + 36 = 37
3² + 7² = 9 + 49 = 58
5² + 8² = 25 + 64 = 89
…
Esse processo leva a um ciclo que se repete (4, 16, 37, 58, 89, 145, 42, 20), retornando a 4 a seguir, e nunca chega a 1.

Exercício: Criar uma rotina para checar se um número é feliz ou não.

Vamos mostrar um pouco do código aqui, no caso, escrito em Python. Nota: como o Python depende da formatação (espaço, tab), a mesma pode se perder transcrito aqui.

Primeiro, uma subrotina para retornar o soma dos dígitos ao quadrado. Uma forma possível é converter o número em string, ler cada dígito, converter em número novamente e fazer a conta, porém, é menos eficiente do que trabalhar diretamente com números, sem converter nada, como abaixo.

def sumSquared(n):
 k=0
 while n>0:
    k += (n % 10)*(n % 10)
    n = int(n/10)
 return(k)

A seguir, utilizamos o somarquadrado para iterar no número e dizer se ele é feliz ou não. Retorna True ou False para indicar se é feliz, e o tamanho do ciclo.



def happyNumber(n):
 setN = set()
 while n>1 and n not in setN:
    setN.add(n)
    n = sumSquared(n)
 return n==1, len(setN)

O código seguinte verifica se os números de 1 a N são felizes ou não, e armazena o resultado.

def procuraHappy(N):
 lstHappy =[]
 lstLength =[]
 lstLenHappy=[]
 for i in range(1,N):
  isHappy, lenN = happyNumber(i)
  lstLength.append(lenN)
  if isHappy:
   lstHappy.append(i)
   lstLenHappy.append(lenN)

A rotina retorna uma lista de números felizes, como os da lista abaixo.

[1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79]

O código a seguir é para visualizar resultados.


import matplotlib.pyplot as plt
#Plota tamanhos do ciclo apenas do happy
plt.figure(figsize=(15,10))
plt.scatter(lstHappy, lstLenHappy,color='goldenrod',marker='.')
plt.title("Tamanhos do ciclo - apenas Números Felizes")
plt.savefig("ApenasHappyCartesian.png")

No gráfico, estão plotados o tamanho do ciclo no eixo y, para cada número Feliz no eixo x, até o número 10.000. Nota-se que há um padrão: o ciclo vai de 1 a 6 no intervalo testado, o que mostra que a convergência é bem rápida.

Vamos plotar todos os tamanhos dos ciclos, independente dos números serem felizes ou não.

#Plota tamanhos do ciclo totais
plt.figure(figsize=(15,10))
x = range(1,N) 
plt.scatter(x, lstLength,color='darkgreen',marker='.')
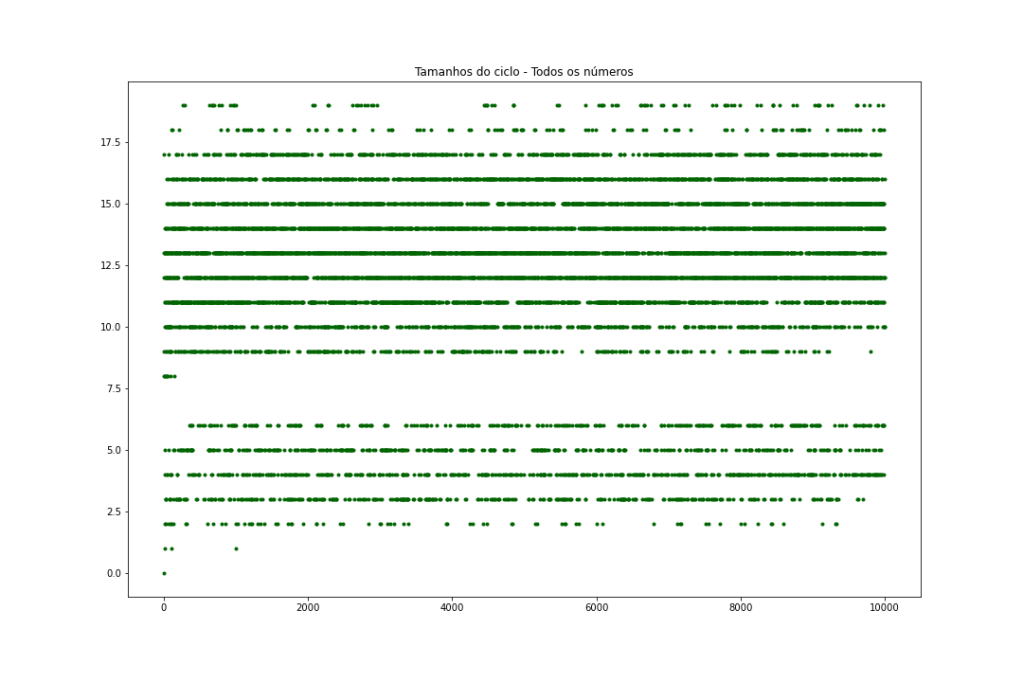
plt.title("Tamanhos do ciclo - Todos os números")
plt.savefig("TodosCartesian.png")

Neste caso, os ciclos são mais longos, podendo chegar a 19 iterações até o ciclo se repetir. Mesmo assim, são números de certa forma comportados. Não é como na conjectura de Collatz, por exemplo, que de vez em quando necessita de centenas de iterações.

Agora, a ideia é transformar os dados numa escala polar, só para visualizar de outra forma.

#Transformando o eixo x numa escala polar
#a cada ciclo de 100, dá uma volta completa
xr =[]
lstHappyPolar =[]
for k in x:
 xr.append(2*math.pi*k/100)

for k in lstHappy:
 lstHappyPolar.append(2*math.pi*k/100)


#Plota tamanhos do ciclo apenas do happy
plt.figure(figsize=(15,10))
plt.polar(lstHappyPolar, lstLenHappy,color='goldenrod',marker='.',linestyle='none')
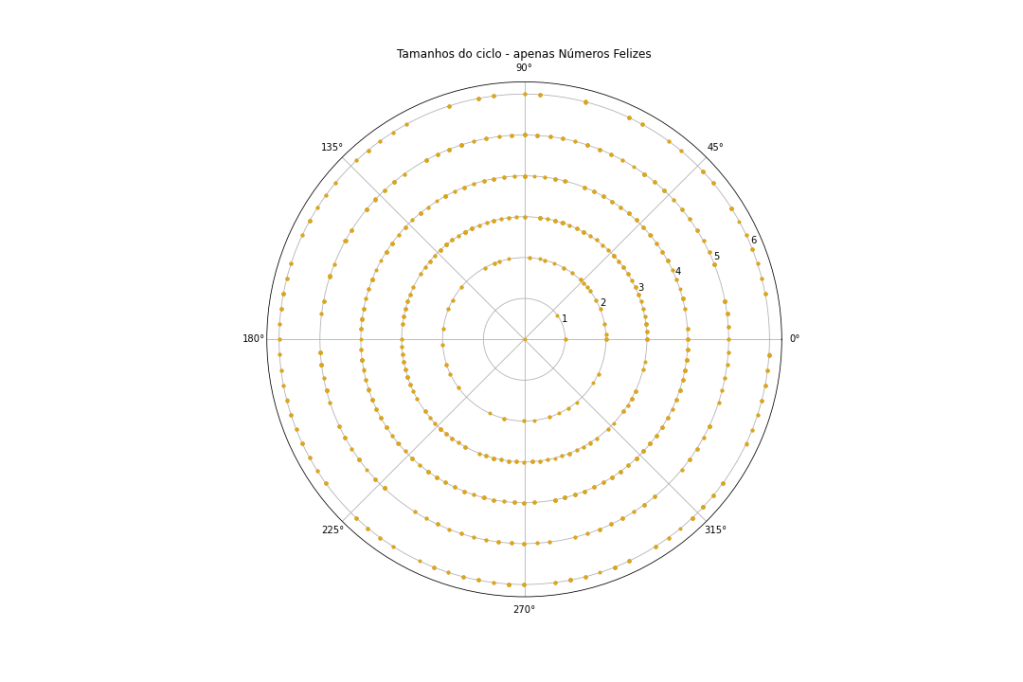
plt.title("Tamanhos do ciclo - apenas Números Felizes")
plt.savefig("apenasHappyPolar.png")

Este gráfico representa os números Felizes. O ângulo é arbitrário, indo de zero a 360 graus para x = 100, e se repetindo. E o raio é o tamanho do ciclo de cada número.

#Plota tamanhos do ciclo todos
plt.figure(figsize=(15,10))
plt.polar(xr, lstLength,color='darkgreen',marker='.',linestyle='none')
plt.title("Tamanhos do ciclo - Todos os números")
plt.savefig("TodosPolar.png")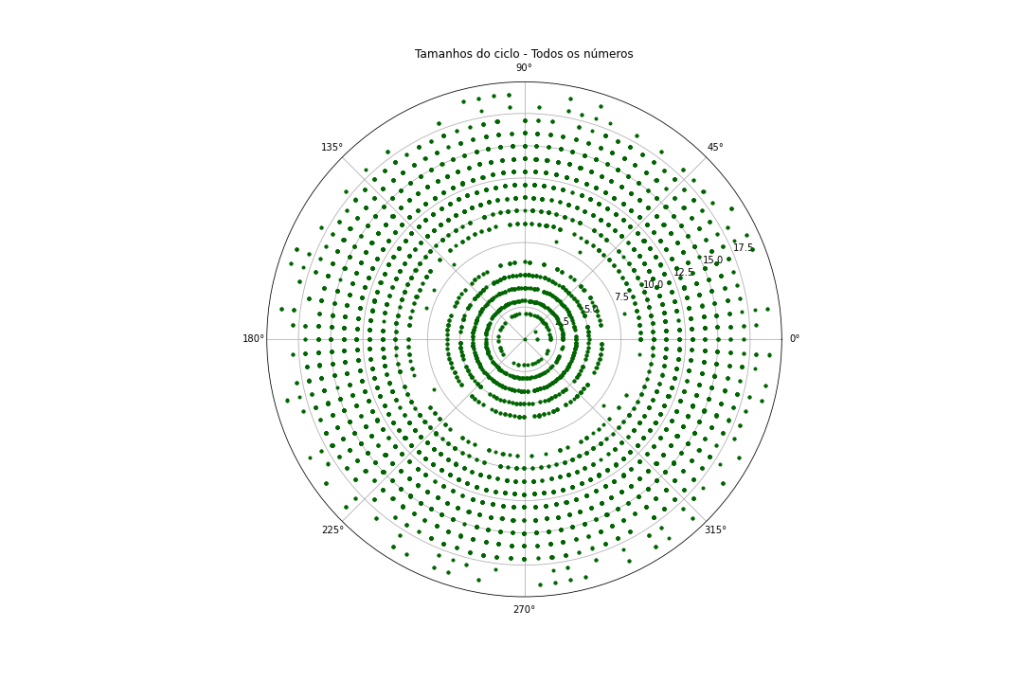

Por fim, no link, uma rotina em Javascript para formatar em amarelo ouro os números felizes. O efeito final é bem legal, provavelmente deixará os números mais felizes ainda!