A Entropia é um conceito fascinante. Vamos aprender um pouco mais sobre o tema, no contexto da Teoria da Informação?

Entropia é uma medida da desordem em um sistema. Desordem mesmo, bagunça.

Imagine um quarto arrumado onde tudo está no seu lugar. Com o tempo, se ninguém arrumar, o quarto tende a ficar bagunçado. Essa tendência natural para a desordem é o que chamamos de entropia.

A desordem, bagunça, têm relação com incerteza.

Num quarto arrumadinho, eu sei que vou encontrar o caderno na mesa da escrivaninha e a calculadora na primeira gaveta. Num quarto todo bagunçado, vai talvez o caderno esteja em cima na gaveta, na mesa, na cama, não sei!

A beleza é mensurar tudo isso, o que acontece através da fórmula a seguir.

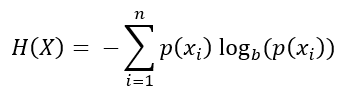
onde:

• H(X) é a entropia da variável aleatória X,
• p(xi) é a probabilidade do evento xi,
• log é o logaritmo na base p (geralmente base 2, resultando em entropia medida em bits).

Vamos fazer um exemplo. No caso do quarto arrumado, vamos ter 100% de certeza de que o caderno estará na mesa da escrivaninha. A entropia será:

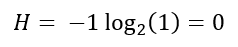
Porque o logaritmo de 1 é igual a zero – ou seja, 2^0 = 1.

A entropia é igual a zero porque tenho certeza de que vou encontrar o caderno lá. Incerteza zero, desordem zero.

Agora, se o caderno tiver 50% de chance de estar na mesa e 50% de chance de estar na gaveta, a entropia será:

A entropia é igual a 1, que é maior do que tínhamos na situação anterior (zero).

E daí também notamos para que serve o sinal negativo. Como estamos fazendo log de um número entre 0 e 1 (pois é uma probabilidade), o valor resultante será negativo. E o sinal de menos é para transformar em positivo.

Agora, se o caderno tiver 25% de chance de estar na mesa e 25% de chance de estar na gaveta, 25% de estar no guarda-roupas e 25% de estar na estante, a entropia será:

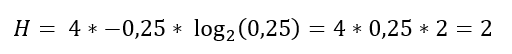
Assim, a entropia é igual a 2.

Como utilizamos log base 2, a medida da incerteza é em bits. Isso é válido principalmente no contexto de comunicação.

Um bit assume valor 0 ou 1. É a quantidade de informação necessária para distinguir entre duas possibilidades. Imagine que vou enviar uma mensagem através de um canal ruidoso, vou precisar de mais bits para compensar essa incerteza.

A entropia da informação é fundamental em áreas como compressão de dados, criptografia e teoria da comunicação.

Quanto mais imprevisível é uma mensagem, maior é a sua entropia.